
如图,已知AB=AC,∠A=36°,AC的垂直平分线MN交AB于D,AC于M.以下结论:
①△BCD是等腰三角形;②射线CD是△ACB的角平分线;③△BCD的周长C△BCD=AB+BC;④△ADM≌△BCD.
正确的有()
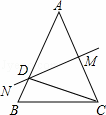
A. ①② B. ①③ C. ②③ D. ③④
B 解:∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∵AC的垂直平分线MN交AB于D,
∴DA=DC,
∴∠ACD=∠A=36°,
∴∠BCD=72°﹣36°=36°,
∴∠BDC=180°﹣∠B﹣∠BCD=72°,
∴CB=CD,
∴△BCD是等腰三角形,所以①正确;
∵∠BCD=36°,∠ACD=36°,
∴CD平分∠ACB,
∴线段CD为△ACB的角平分线,所以②错误;
∵DA=DC,
∴△BCD的周长C△BCD=DB+DC+BC=DB+DA+BC=AB+BC,所以③正确;
∵△ADM为直角三角形,而△BCD为顶角为36°的等腰三角形,
∴△ADM不等全等于△BCD,所以④错误.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
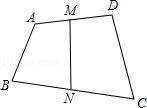
已知:四边形ABCD中,AB=2,CD=3,M、N分别是AD,BC的中点,则线段MN的取值范围是( )
A.1<MN<5 B.1<MN≤5
C.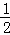 <MN<
<MN<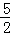 D.
D.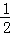 <MN≤
<MN≤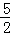
查看答案和解析>>
科目:初中数学 来源: 题型:
如图(1),在等边△ABC的顶点B、C处各有一只蜗牛,它们同时出发分别以每分钟1各单位的速度油B向C和由C向A爬行,其中一只蜗牛爬到终点s时,另一只也停止运动,经过t分钟后,它们分别爬行到D,P处,请问:
(1)在爬行过程中,BD和AP始终相等吗?为什么?
(2)问蜗牛在爬行过程中BD与AP所成的∠DQA大小有无变化?请证明你的结论.
(3)若蜗牛沿着BC和CA的延长线爬行,BD与AP交于点Q,其他条件不变,如图(2)所示,蜗牛爬行过程中的∠DQA大小变化了吗?若无变化,请证明.若有变化,请直接写出∠DQA的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
证明:猜想∠A与∠C关系为:∠A+∠C=180°.
连结AC,

∵∠ABC=90°,
∴在Rt△ABC中,由勾股定理得:
AC= =25cm,
=25cm,
∵AD2+DC2=625=252=AC2,
∴△ADC是直角三角形,且∠D=90°,
∵∠DAB+∠B+∠BCD+∠D=180°,
∴∠DAB+∠BCD=180°,
即∠A+∠C=180°.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com