证明：猜想∠A与∠C关系为：∠A+∠C=180°．
连结AC，
∵∠ABC=90°，
∴在Rt△ABC中，由勾股定理得：
AC=
=25cm，
∵AD2+DC2=625=252=AC2，
∴△ADC是直角三角形，且∠D=90°，
∵∠DAB+∠B+∠BCD+∠D=180°，
∴∠DAB+∠BCD=180°，
即∠A+∠C=180°．
科目：初中数学 来源： 题型：
如图，边长为n的正方形OABC的边OA，OC在坐标轴上，点A1，A2…,An﹣1为OA的n等分点，点B1，
B2.,….Bn﹣1为CB的n等分点，连结A1B1，A2B2，…An﹣1Bn﹣1，分别交曲线
（x＞0）于点C1，C2，…，Cn﹣1．若C15B15=16C15A15，则n的值为 ．（n为正整数）
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，四边形ABCD是平行四边形，∠D=120°，∠CAD=32°，则∠ABC、∠CAB的度数分别为（）
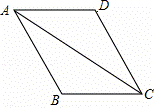
A． 28°，120° B． 120°，28° C． 32°，120° D． 120°，32°
查看答案和解析>>
科目：初中数学 来源： 题型：
5cm≤h≤6cm 解：∵将一根长为18cm的筷子，置于底面直径为5cm，高为12cm的圆柱形水杯中，
∴在杯子中筷子最短是等于杯子的高，最长是等于杯子斜边长度，
∴当杯子中筷子最短是等于杯子的高时，x=12，
最长时等于杯子斜边长度是：x=
=13，
∴h的取值范围是：（18﹣13）cm≤h≤（18﹣12）cm，
即5cm≤h≤6cm．
故答案为：5cm≤h≤6cm．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，四边形ABCD是正方形，点G是BC边上任意一点，DE⊥AG于点E，BF∥DE且交AG于点F．
（1
）求证：AE=BF；
（2）如图1，连接DF、CE，探究线段DF与CE的关系并证明；
（3）如图2，若AB=
，G为CB中点，连接CF，直接写出四边形CDEF的面积为3．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，已知AB=AC，∠A=36°，AC的垂直平分线MN交AB于D，AC于M．以下结论：
①△BCD是等腰三角形；②射线CD是△ACB的角平分线；③△BCD的周长C△BCD=AB+BC；④△ADM≌△BCD．
正确的有（）
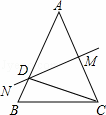
A． ①② B． ①③ C． ②③ D． ③④
查看答案和解析>>
科目：初中数学 来源： 题型：
小杰到学校食堂买饭，看到
A、B两窗口前面排队的人一样多（设为a人，a＞8），就站在A窗口队伍的后面，过了2分钟，他发现A窗口每分钟有4人买了饭离开队伍，B窗口每分钟有6人买了饭离开队伍，且B窗口队伍后面每分钟增加5人．
（1）此时，若小杰继续在A窗口排队，则他到达窗口所花的时间是多少？（用含a的代数式表示）
（2）此时，若小杰迅速从A窗口队伍转移到B窗口后面重新排队，且到达B窗口所花的时间比继续在A窗口排队到达A窗口所花的时间少，求a的取值范围．（不考虑其它因素）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
；
_____