
如图(1),在等边△ABC的顶点B、C处各有一只蜗牛,它们同时出发分别以每分钟1各单位的速度油B向C和由C向A爬行,其中一只蜗牛爬到终点s时,另一只也停止运动,经过t分钟后,它们分别爬行到D,P处,请问:
(1)在爬行过程中,BD和AP始终相等吗?为什么?
(2)问蜗牛在爬行过程中BD与AP所成的∠DQA大小有无变化?请证明你的结论.
(3)若蜗牛沿着BC和CA的延长线爬行,BD与AP交于点Q,其他条件不变,如图(2)所示,蜗牛爬行过程中的∠DQA大小变化了吗?若无变化,请证明.若有变化,请直接写出∠DQA的度数.

解:(1)在爬行过程中,BD和AP始终相等,
理由是:∵△ABC是等边三角形,
∴∠CAB=∠C=∠ABP=60°,AB=BC,
在△BDC和△APB中,
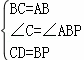 ,
,
∴△BDC≌△APB(SAS),
∴BD=AP.
(2)蜗牛在爬行过程中BD与AP所成的∠DQA大小无变化,
理由:∵△BDC≌△APB,
∴∠CBD=∠BAP,
∴∠DQA=∠DBA+∠BAP=∠DBA+∠CBD=∠ABC=60°,
即蜗牛在爬行过程中BD与AP所成的∠DQA大小无变化,始终是60°.
(3)蜗牛爬行过程中的∠DQA大小无变化,
理由是:根据题意得:BP=CD,
∵BC=AC,
∴CP=AD,
∵△ABC是等边三角形,
∴AC=AB,∠CAB=∠ACB=6 0°,
0°,
∵∠ACP+∠ACB=180°,∠DAB+∠CAB=180°,
∴∠ACP=∠BAD,
在△ABD和△ACP中,
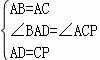 ,
,
∴△ABD≌△ACP(SAS),
∴∠CAP=∠ABD,
∴∠AQD=∠ABD+∠BAQ=∠CAP+∠QAB
=180°﹣∠CAB
=180°﹣60°
=120°,
即蜗牛爬行过程中的∠DQA无变化,等于120°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
如图,四边形ABCD是平行四边形,∠D=120°,∠CAD=32°,则∠ABC、∠CAB的度数分别为()
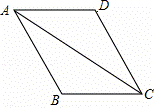
A. 28°,120° B. 120°,28° C. 32°,120° D. 120°,32°
查看答案和解析>>
科目:初中数学 来源: 题型:
5cm≤h≤6cm 解:∵将一根长为18cm的筷子,置于底面直径为5cm,高为12cm的圆柱形水杯中,
∴在杯子中筷子最短是等于杯子的高,最长是等于杯子斜边长度,
∴当杯子中筷子最短是等于杯子的高时,x=12,
最长时等于杯子斜边长度是:x= =13,
=13,
∴h的取值范围是:(18﹣13)cm≤h≤(18﹣12)cm,
即5cm≤h≤6cm.
故答案为:5cm≤h≤6cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,已知AB=AC,∠A=36°,AC的垂直平分线MN交AB于D,AC于M.以下结论:
①△BCD是等腰三角形;②射线CD是△ACB的角平分线;③△BCD的周长C△BCD=AB+BC;④△ADM≌△BCD.
正确的有()
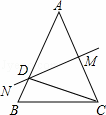
A. ①② B. ①③ C. ②③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
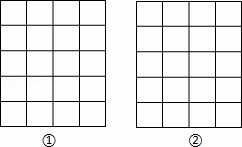
如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点,以格点为顶点按下列要求画图:
(1)在图中画一条线段MN,使MN= ;
;
(2)在图‚中画一个三边长均为无理数,且各边都不相等的直角△DEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com