
【题目】2a2+[a2+(3a2-2a)-2(a2-3a)] 其中a=- ![]() .
.
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,直线AB与x轴y轴分别交于A,B两点,与双曲线y= ![]() 在第一象限内交于点C,BO=2AO=4,△AOC的面积为2
在第一象限内交于点C,BO=2AO=4,△AOC的面积为2 ![]() +2.
+2. 
(1)求点C的坐标和k的值;
(2)若点P在双曲线y= ![]() 上,点Q在y轴上,且以A,B,P,Q为顶点的四边形为平行四边形,求所有符合题意的点Q的坐标.
上,点Q在y轴上,且以A,B,P,Q为顶点的四边形为平行四边形,求所有符合题意的点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
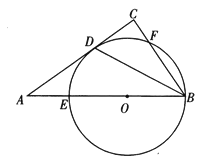
【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,与AC交于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.
(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,∠3=∠4,∠BOD= ![]() ∠AOB=90°.下列判断:①射线OF是∠BOE的角平分线;②∠DOE的补角是∠BOC;③∠AOC的余角只有∠COD;④∠DOE的余角有∠BOE和∠COD;⑤∠COD=∠BOE.其中正确的有( )
∠AOB=90°.下列判断:①射线OF是∠BOE的角平分线;②∠DOE的补角是∠BOC;③∠AOC的余角只有∠COD;④∠DOE的余角有∠BOE和∠COD;⑤∠COD=∠BOE.其中正确的有( )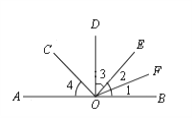
A.5个
B.4个
C.3个
D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3s后,两点相距18个单位长度.已知点B的速度是点A的速度的5倍(速度单位:单位长度/s).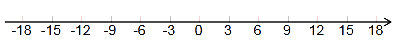
(1)求出点A、点B运动的速度,并在数轴上标出A,B两点从原点出发运动3s时的位置;
(2)若A,B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)当A,B两点从(2)中的位置继续以原来的速度沿数轴向左运动的同时,另一点C从原点位置也向点A运动,当遇到点A后,立即返回向点B运动,遇到点B后又立即返回向点A运动,如此往返,直到点B追上点A时,点C立即停止运动.若点C一直以8个单位长度/s的速度匀速运动,则点C从开始运动到停止运动,行驶的路程是多少个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a3(3an-2am+4ak)=3a9-2a6+4a4,则m,n,k的值分别为( )
A. 6,3,1 B. 3,6,1 C. 2,1,3 D. 2,3,1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=75°,则∠NPB′=°.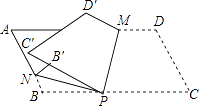
查看答案和解析>>
科目:初中数学 来源: 题型:
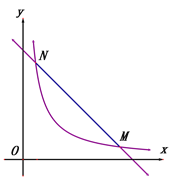
【题目】已知直线![]() (k>0)与双曲线
(k>0)与双曲线![]() (x>0)交于点M、N,且点N的横坐标为k. .
(x>0)交于点M、N,且点N的横坐标为k. .
(1) 如图1,当k=1时.
①求m的值及线段MN的长;
②在y轴上是否是否存在点Q,使∠MQN=90°,若存在,请求出点Q的坐标;若不存在,请说明理由.
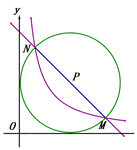
(2) 如图2,以MN为直径作⊙P,当⊙P与y轴相切时,求k值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com