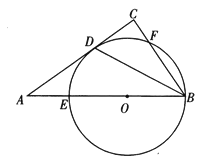
【题目】如图，在Rt△ABC中，∠C=90°，BD平分∠ABC，与AC交于点D，点O是AB上一点，⊙O过B、D两点，且分别交AB、BC于点E、F．

（1）求证：AC是⊙O的切线；

（2）已知AB=10，BC=6，求⊙O的半径r．

参考答案：

【答案】（1）证明见解析；（2）.

【解析】试题分析：（1）连接OD．欲证AC是⊙O的切线，只需证明AC⊥OD即可；

（2）利用平行线截线段成比例推知；然后将图中线段间的和差关系代入该比例式，通过解方程即可求得r的值，即⊙O的半径r的值．

试题解析：（1）证明：连接OD．

∵OB=OD，

∴∠OBD=∠ODB（等角对等边）；

∵BD平分∠ABC，

∴∠ABD=∠DBC，

∴∠ODB=∠DBC（等量代换），

∴OD∥BC（内错角相等，两直线平行）；

又∵∠C=90°（已知），

∴∠ADO=90°（两直线平行，同位角相等），

∴AC⊥OD，即AC是⊙O的切线；

（2）解：由（1）知，OD∥BC，

∴（平行线截线段成比例），

∴，

解得r=，即⊙O的半径r为．

关闭