
【题目】如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H, 
(1)求∠ACB的度数;
(2)HE= ![]() AF.
AF.
【答案】
(1)解:∵AB=AC,
∴∠ACB=∠ABC,
∵∠BAC=45°,
∴∠ACB=∠ABC= ![]() (180°﹣∠BAC)=
(180°﹣∠BAC)= ![]() (180°﹣45°)=67.5°
(180°﹣45°)=67.5°
(2)解:连结HB,
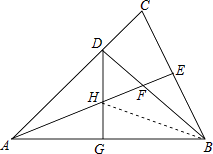
∵AB=AC,AE平分∠BAC,
∴AE⊥BC,BE=CE,
∴∠CAE+∠C=90°,
∵BD⊥AC,
∴∠CBD+∠C=90°,
∴∠CAE=∠CBD,
∵BD⊥AC,D为垂足,
∴∠DAB+∠DBA=90°,
∵∠DAB=45°,
∴∠DBA=45°,
∴∠DBA=∠DAB,
∴DA=DB,
在Rt△BDC和Rt△ADF中,
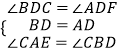
∴Rt△BDC≌Rt△ADF (ASA),
∴BC=AF,
∵DA=DB,点G为AB的中点,
∴DG垂直平分AB,
∵点H在DG上,
∴HA=HB,
∴∠HAB=∠HBA= ![]() ∠BAC=22.5°,
∠BAC=22.5°,
∴∠BHE=∠HAB+∠HBA=45°,
∴∠HBE=∠ABC﹣∠ABH=67.5°﹣22.5°=45°,
∴∠BHE=∠HBE,
∴HE=BE= ![]() BC,
BC,
∵AF=BC,
∴HE= ![]() AF
AF
【解析】(1)根据等腰三角形性质和三角形内角和定理求出即可;(2)证△ADF≌△BDC,推出AF=BC,求出HE=BE=CE,即可得出答案.


科目:初中数学 来源: 题型:
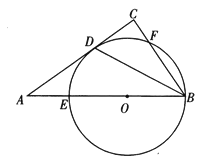
【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,与AC交于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.
(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是平行四边形纸片ABCD的BC边上一点,以过点P的直线为折痕折叠纸片,使点C,D落在纸片所在平面上C′,D′处,折痕与AD边交于点M;再以过点P的直线为折痕折叠纸片,使点B恰好落在C′P边上B′处,折痕与AB边交于点N.若∠MPC=75°,则∠NPB′=°.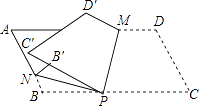
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列叙述正确的是( )
A. 平分弦的直径必垂直于弦 B. 三角形的外心到三边的距离相等
C. 相等的圆心角所对的弧相等 D. 垂直平分弦的直线必平分这条弦所对的弧
查看答案和解析>>
科目:初中数学 来源: 题型:
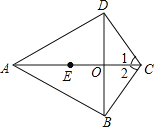
【题目】如图,在四边形ABCD中,AB=AD,BC=DC,AC、BD相交于点O,点E在AO上,且OE=OC.
(1)求证:∠1=∠2;
(2)连结BE、DE,判断四边形BCDE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:
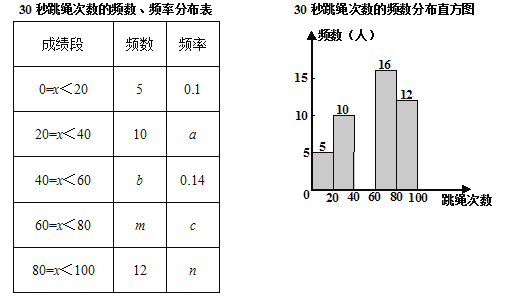
根据以上图表信息,解答下列问题:
(1)表中的a= ,m= ;
(2)请把频数分布直方图补充完整;(画图后请标注相应的数据)
(3)若该校九年级共有600名学生,请你估计“30秒跳绳”的次数60次以上(含60次)的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() (k>0)与双曲线
(k>0)与双曲线![]() (x>0)交于点M、N,且点N的横坐标为k. .
(x>0)交于点M、N,且点N的横坐标为k. .
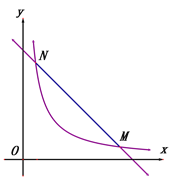
(1) 如图1,当k=1时.
①求m的值及线段MN的长;
②在y轴上是否是否存在点Q,使∠MQN=90°,若存在,请求出点Q的坐标;若不存在,请说明理由.
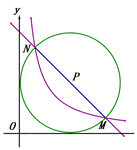
(2) 如图2,以MN为直径作⊙P,当⊙P与y轴相切时,求k值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M. 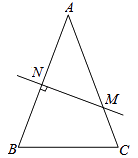
(1)若∠B=70°,则∠NMA的度数是 .
(2)连接MB,若AB=8cm,△MBC的周长是14cm.
①求BC的长;
②在直线MN上是否存在点P,使由P,B,C构成的△PBC的周长值最小?若存在,标出点P的位置并求△PBC的周长最小值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com