
����Ŀ������ABC�У�CA��CB������AED�У� DA��DE����D��E�ֱ���CA��AB�ϣ�
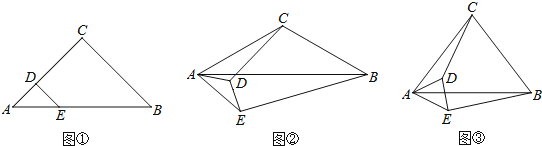
��1����ͼ�٣�����ACB����ADE��90������CD��BE��������ϵ�� ��
��2������ACB����ADE��120��������AED�Ƶ�A��ת����ͼ����ʾ��λ�ã���CD��BE��������ϵ��
��3������ACB����ADE��2����0��< �� < 90����������AED�Ƶ�A��ת����ͼ����ʾ��λ�ã�̽���߶�CD��BE��������ϵ��������֤��(�ú�����ʽ�ӱ�ʾ)��
���𰸡���1��BE��![]() CD����2��BE��
CD����2��BE��![]() CD����3��BE=2CD��sin����֤����������
CD����3��BE=2CD��sin����֤����������
�������������������1������֪����ADE����ACB���ǵ���ֱ�������Σ�������AE=![]() AD��AB=
AD��AB=![]() AC���Ӷ���
AC���Ӷ���![]() ����BE��
����BE��![]() CD.
CD.
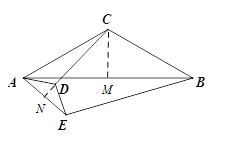
��2����ͼ���ֱ����C��D��CM��AB�ڵ�M��DN��AE�ڵ�N��
��CA��CB��DA��DE����ACB����ADE=120����
���CAB����DAE����ACM����ADN="60��" ��AM=![]() AB��AN=
AB��AN=![]() AE��
AE��
���CAD����BAE��
��Rt��ACM��Rt��ADN��sin��ACM=![]() =
=![]() ��sin��ADN=
��sin��ADN=![]() =
=![]() ��
��
��![]() ����
����![]() ��
��
���ߡ�CAD����BAE�����BAE�ס�CAD����![]() .��BE��
.��BE��![]() CD��
CD��
��3�����ݵ��������ε����ʺ�������Ǻ����������![]() ��������BAE�ס�CAD�ó�
��������BAE�ס�CAD�ó�![]() ���Ӷ��ó�����.
���Ӷ��ó�����.
��1��BE��![]() CD.
CD.
��2��BE��![]() CD.
CD.
��3��BE=2CD��sin����֤�����£�
��ͼ���ֱ����C��D��CM��AB�ڵ�M��DN��AE�ڵ�N��
��CA��CB��DA��DE����ACB����ADE="2��" ��
���CAB����DAE����ACM����ADN="��" ��AM=![]() AB��AN=
AB��AN=![]() AE��
AE��
���CAD����BAE��
��Rt��ACM��Rt��ADN��sin��ACM=![]() ��sin��ADN=
��sin��ADN=![]() ��
��
��![]() ����
����![]() ��
��
���ߡ�CAD����BAE�����BAE�ס�CAD����![]() .
.
��BE=2DC��sin����



 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ��P��ʾ������6���Ȱ�����������ƶ�3����λ���ȣ��������ƶ�5����λ���ȣ����P��ʾ������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼһ������ABCD�У�AB=5cm��BC=4cm��E��BC��һ�㣬����CDE��DE�۵���ʹ��C����AB��һ��F��������DF��EF�� 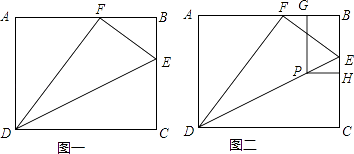
��1����BE�ij��ȣ�
��2�����P��H��G�ֱ����߶�DE��BC��BA�ϣ���BP=CP���ı���BGPHΪ����ʱ����˵������BGPH�ij�����Ϊ2��1������PE�ij�������ͼ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ʒÿ���ɱ�10Ԫ��������ÿ����Ʒ�����ۼ�x��Ԫ�����Ʒ����������y������֮��Ĺ�ϵ���±���
x ��Ԫ�� | 15 | 20 | 25 | �� |
y ������ | 25 | 20 | 15 | �� |
����������y�����ۼ�x��һ�κ�����
��1�������������y�����������ۼ�x��Ԫ���ĺ�����ϵʽ��
��2�������ۼ۶�Ϊ30Ԫʱ��ÿ�յ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������෴����ƽ���������������������������������( )
A. ��1B. 1C. 0D. ��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ���������������˵���߶���ɵ�һ���������Ұ��������߷ֳɳ�����ȵ������֣��������������ߵ������е�������ͼ����D������A��C��B�������е����������������⣺

��1����AC��BCʱ����D���߶��� �ϣ� ��AC��BCʱ����D���� ���غϣ���AC��BCʱ����D���߶��� ���ϣ�
��2����AC��18cm,BC��10cm,����ACB=90��,��һ����P��C����������߶�CB�����B�˶����ٶ�Ϊ2cm/s, ���˶�ʱ����t��s��, ��tΪ��ֵ��������PCD �����Ϊ10![]() ��
��
��3����EΪ�߶�AC�е㣬EC��8cm��CD��6cm����CB�ij��ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
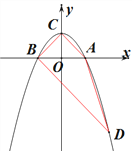
����Ŀ����ͼ��������y=ax2+b��x�ύ�ڵ�A��B����A�������Ϊ��1��0������y�ύ�ڵ�C��0��1��
��1���������ߵĽ���ʽ���������B���ꣻ
��2������B��BD��CA���������ڵ�D������BC��CA��AD�����ı���ABCD���ܳ������������������
��3����x���Ϸ������������Ƿ���ڵ�P������P��PE��ֱ��x�ᣬ����Ϊ��E��ʹ��B��P��EΪ���������������CBD���ƣ������������P������ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com