
【题目】如图一,矩形ABCD中,AB=5cm,BC=4cm,E是BC上一点,将△CDE沿DE折叠,使点C落在AB上一点F处,连结DF、EF. 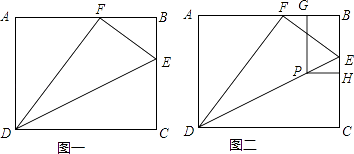
(1)求BE的长度;
(2)设点P、H、G分别在线段DE、BC、BA上,当BP=CP且四边形BGPH为矩形时,请说明矩形BGPH的长宽比为2:1,并求PE的长.(如图二)
【答案】
(1)解:如图一,
在矩形ABCD中,AD=BC=4,CD=AB=5,∠A=90°,
由折叠可得:DF=DC=5,CE=CF,
∴直角三角形ADF中,AF= ![]() =3,
=3,
∴BF=5=3=2,
设BE=x,则CE=FE=4﹣x,
在Rt△BEF中,22+x2=(4﹣x)2,
解得x=1.5,
即BE=1.5
(2)解:如图二,当BP=CP,且四边形BGPH为矩形时,点P在BC的垂直平分线上,
即PH垂直平分BC,
∴BH=CH= ![]() BC=2,①
BC=2,①
又∵BE=1.5,
∴EH=0.5,EC=2.5
∵PH∥DC,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]()
解得PH=1,②
∴由①②得:矩形BGPH的长宽比为2:1,
在Rt△PEH中,PE= ![]() =
= ![]() =
= ![]()
【解析】(1)先根据矩形性质以及折叠变换,运用勾股定理求得AF、BF的长,再设BE=x,在Rt△BEF中运用勾股定理列出方程,求得x的值.(2)先判断PH垂直平分BC,求得矩形中BH的长,再根据平行线分线段成比例定理,求得PH的长,进而得出矩形BGPH的长宽比为2:1,最后根据勾股定理求得PE的长.
【考点精析】利用勾股定理的概念和矩形的性质对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;矩形的四个角都是直角,矩形的对角线相等.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,为了躲避台风,一轮船一直由西向东航行,上午10点,在A处测得小岛P的方向是北偏东75°,以每小时15海里的速度继续向东航行,中午12点到达B处,并测得小岛P的方向是北偏东60°,若小岛周围25海里内有暗礁,问该轮船是否能一直向东航行? 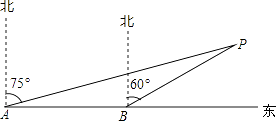
查看答案和解析>>
科目:初中数学 来源: 题型:
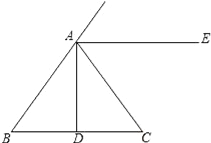
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,AE∥BC.
(1)作∠ADC的平分线DF,与AE交于点F;(用尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若AD=2,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AD=2,E是AB的中点,将△BEC绕点B逆时针旋转90°后,点E落在CB的延长线上点F处,点C落在点A处.再将线段AF绕点F顺时针旋转90°得线段FG,连接EF,CG. 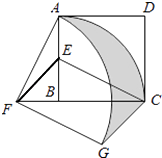
(1)求证:EF∥CG;
(2)求点C,点A在旋转过程中形成的 ![]() ,
, ![]() 与线段CG所围成的阴影部分的面积.
与线段CG所围成的阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
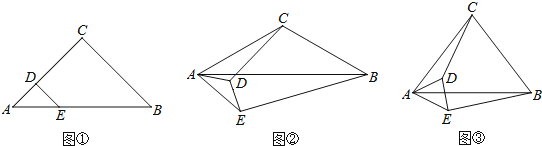
【题目】在△ABC中,CA=CB,在△AED中, DA=DE,点D、E分别在CA、AB上.
(1)如图①,若∠ACB=∠ADE=90°,则CD与BE的数量关系是 ;
(2)若∠ACB=∠ADE=120°,将△AED绕点A旋转至如图②所示的位置,求CD与BE的数量关系;
(3)若∠ACB=∠ADE=2α(0°< α < 90°),将△AED绕点A旋转至如图③所示的位置,探究线段CD与BE的数量关系,并加以证明(用含α的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的多项式
的多项式![]() ,其
,其![]() ,
, ![]() ,
, ![]() ,
, ![]() 为互不相等的整数,且
为互不相等的整数,且![]() .
.
(![]() )求
)求![]() 的值.
的值.
(![]() )当
)当![]() 时,这个多项式
时,这个多项式![]() 的值为
的值为![]() .求
.求![]() 的值.
的值.
(![]() )当
)当![]() 时,求这个多项式
时,求这个多项式![]() 的所有可能的值.
的所有可能的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com