
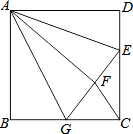
 如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:
如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG,CF.下列结论:| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
分析 在直角三角形EGC中,根据勾股定理可证BG=CG,通过证明∠ABG+∠AGF=2∠AGB=180°-∠FGC=∠GFC+∠GCF=2∠GCF,可证CF∥AG,根据平行线的性质可证∠AGB=∠GCF≠60°,即可证得FG≠FC,根据∠FEC+∠FGC=90°,∠FCE+∠FCG=90°,∠FGC≠∠FCG,可知∠FEC≠FCE,证得EF≠FC,根据∠BAG+∠DAE=∠FAG+∠FAE=∠GAE,∠BAG+∠DAE+∠GAE=90°,即可证得∠GAE=45°,由S△GFC:S△FCE=$\frac{3}{2}$:1=3:2,S△GCE=$\frac{1}{2}$GC•CE=$\frac{1}{2}$×$\frac{3}{2}$×2=$\frac{3}{2}$,即可求得S△FGC=$\frac{3}{5}$×$\frac{3}{2}$=$\frac{9}{10}$.
解答 解:∵四边形ABCD是正方形,
∴CD=AB=3,
∵CD=3DE,
∴DE=1,
∴EF=DE=1,
∴EC=2,
在RT△ABG和RT△AFG中
$\left\{\begin{array}{l}{AB=AF}\\{AG=AG}\end{array}\right.$
∴RT△ABG≌RT△AFG(HL),
∴BG=FG,
设BG=FG=x,则CG=3-x,
在RT△ECG中,EG2=CG2+CE2,
即(x+1)2=(3-x)2+22,解得x=$\frac{3}{2}$,
∴BG=$\frac{3}{2}$=3-$\frac{3}{2}$=CG,
∴G是BC中点;故①正确;
∵GF=GC,
∴∠GCF=∠GFC,
∵RT△ABG≌RT△AFG,
∴∠AGB=∠AGF,
∴∠ABG+∠AGF=2∠AGB=180°-∠FGC=∠GFC+∠GCF=2∠GCF,
∴∠AGB=∠GCF,
∴CF∥AG,
∵tan∠AGB=$\frac{AB}{BG}$=2,
∴∠AGB≠60°,
∴∠GCF≠60°,
∴△GCF不是等边三角形,
∴FG≠FC,故②错误;
∵∠FEC+∠FGC=90°,∠FCE+∠FCG=90°,∠FGC≠∠FCG,
∴∠FEC≠FCE,
∴EF≠FC,故③错误;
∵RT△ABG≌RT△AFG,
∴∠BAG=∠FAG,
∵∠DAE=∠FAE,
∴∠BAG+∠DAE=∠FAG+∠FAE=∠GAE,
∵∠BAG+∠DAE+∠GAE=90°,
∴∠GAE=45°,故④正确;
∵S△GCE=$\frac{1}{2}$GC•CE=$\frac{1}{2}$×$\frac{3}{2}$×2=$\frac{3}{2}$,
∵GF=$\frac{3}{2}$,EF=1,
∴S△GFC:S△FCE=$\frac{3}{2}$:1=3:2,
∴S△FGC=$\frac{3}{5}$×$\frac{3}{2}$=$\frac{9}{10}$,故⑤正确;
正确的个数有①④⑤;
故选B.
点评 本题考查了正方形的性质,三角形全等的判定和性质,勾股定理的应用,等边三角形的判定,解直角三角形等,熟练掌握性质定理是解题的关键.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
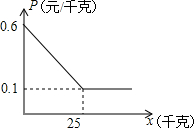 某小贩每天从批发市场买进一定数量的土豆,其价格为每千克0.60元,卖出的价格是每千克0.80元,卖不掉的土豆可卖给附近的餐厅,不过每千克卖出的价格P(元/千克)与卖出的数量x(千克)的关系可近似地用图中的一条折线表示.经过市场调查发现,在一个月内(按30天算)有20天每天可卖出100千克,有10天每天只能卖出70千克,而批发市场规定每天批发给小贩的它的数量必须相同.
某小贩每天从批发市场买进一定数量的土豆,其价格为每千克0.60元,卖出的价格是每千克0.80元,卖不掉的土豆可卖给附近的餐厅,不过每千克卖出的价格P(元/千克)与卖出的数量x(千克)的关系可近似地用图中的一条折线表示.经过市场调查发现,在一个月内(按30天算)有20天每天可卖出100千克,有10天每天只能卖出70千克,而批发市场规定每天批发给小贩的它的数量必须相同.| 所批发土豆的数量x(千克) | 70 | 90 | 100 |
| 每月所得毛利润W(元) | 420 | 540 | 570 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
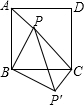 如图,将正方形ABCD中的△ABP绕点B顺时针旋转到△CBP′的位置,且BP=2,AP=1.
如图,将正方形ABCD中的△ABP绕点B顺时针旋转到△CBP′的位置,且BP=2,AP=1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
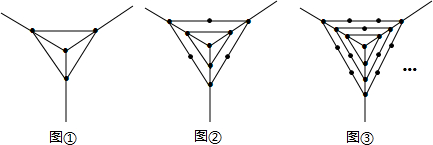
| 图形编号 | ① | ② | ③ | … |
| 图形中点的个数 | 4 | 10 | 19 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com