
【题目】某班为了从甲、乙两同学中选出班长,进行了一次演讲答辩与民主测评.A、B、C、D、E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了民主测评.结果如下表所示:
表1 演讲答辩得分表(单位:分)
A | B | C | D | E | |
甲 | 90 | 92 | 94 | 95 | 88 |
乙 | 89 | 86 | 87 | 94 | 91 |
表2 民主测评票数统计表(单位:张)
“好”票数 | “较好”票数 | “一般”票数 | |
甲 | 40 | 7 | 3 |
乙 | 42 | 4 | 4 |
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;
民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;
综合得分=演讲答辩得分×(1﹣a)+民主测评得分×a(0.5≤a≤0.8).
(1)当a=0.6时,甲的综合得分是多少?
(2)a在什么范围时,甲的综合得分高?a在什么范围时,乙的综合得分高?
【答案】(1)89分(2)当0.5≤a<0.75时,甲的综合得分高,0.75<a≤0.8时,乙的综合得分高
【解析】
(1)由题意可知:分别计算出甲的演讲答辩得分以及甲的民主测评得分,再将a=0.6代入公式计算可以求得甲的综合得分;
(2)同(1)一样先计算出乙的演讲答辩得分以及乙的民主测评得分,则乙的综合得分=89(1a)+88a,甲的综合得分=92(1a)+87a,再分别比较甲、乙的综合得分,甲的综合得分高时即当甲的综合得分>乙的综合得分时,可以求得a的取值范围;同理甲的综合得分高时即当甲的综合得分<乙的综合得分时,可以求得a的取值范围.
(1)甲的演讲答辩得分=![]() =92(分),
=92(分),
甲的民主测评得分=40×2+7×1+3×0=87(分),
当a=0.6时,甲的综合得分=92×(10.6)+87×0.6=36.8+52.2=89(分);
答:当a=0.6时,甲的综合得分是89分;
(2)∵乙的演讲答辩得分=![]() =89(分),
=89(分),
乙的民主测评得分=42×2+4×1+4×0=88(分),
∴乙的综合得分为:89(1a)+88a,甲的综合得分为:92(1a)+87a,
当92(1a)+87a>89(1a)+88a时,即有a<![]() ,
,
又0.5≤a≤0.8,
∴0.5≤a<0.75时,甲的综合得分高;
当92(1a)+87a<89(1a)+88a时,即有a>![]() ,
,
又0.5≤a≤0.8,
∴0.75<a≤0.8时,乙的综合得分高.
答:当0.5≤a<0.75时,甲的综合得分高,0.75<a≤0.8时,乙的综合得分高.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)直接写出点C的坐标.
(2)在y轴上是否存在点P,使得S△POB=![]() S△ABC若存在,求出点P的坐标;若不存在,请说明理由.
S△ABC若存在,求出点P的坐标;若不存在,请说明理由.
(3)把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探究∠HBM,∠BMA,∠MAC之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
(1)如图①,直线m经过平行四边形ABCD对角线的交点O,则S四边形AEFB S四边形DEFC(填“>”“<”“=”);
(2)如图②,两个正方形如图所示摆放,O为小正方形对角线的交点,求作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图③所示摆放,求作直线将整个图形分成面积相等的两部分(用三种方法分割).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴正半轴相交于A、B两点,与y轴相交于点C,对称轴为直线x=2,且OA=OC,则下列结论:①abc>0;②9a+3b+c<0;③c>﹣1;④关于x的方程ax2+bx+c=0(a≠0)有一个根为 -![]() ,其中正确的结论个数有_____________________ (填序号)
,其中正确的结论个数有_____________________ (填序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学决定到超市购买一定数量的羽毛球拍和羽毛球,已知买1副羽毛球拍和1个羽毛球要花费35元,买2副羽毛球拍和3个羽毛球要花费75元,求购买10副羽毛球拍和20个羽毛球共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场准备购进甲.乙两种商品,若购进甲商品80个,乙商品40个,需要800元;若购进甲商品50个,乙商品30个,需要550元.
(1)求商场购进甲.乙两种商品每个需要多少元?
(2)商场准备1000元全部用来购进甲.乙两种商品,计划销售每个甲种商品可获利润4元,销售每个乙种商品可获利润5元,销售这两种玩具的总利润不低于600元,那么商场最多购进乙种商品多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为6,点E,F分别在AB,AD上,若CE=3![]() ,且∠ECF=45°,则CF的长为( )
,且∠ECF=45°,则CF的长为( )

A. 2![]() B. 3
B. 3![]() C.
C. ![]()
![]() D.
D. ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为传承中华优秀传统文化,某校团委组织了一次全校2800名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩(成绩![]() 取整数,总分100分)作为样本进行统计,制成如下不完整的统计图表:
取整数,总分100分)作为样本进行统计,制成如下不完整的统计图表:
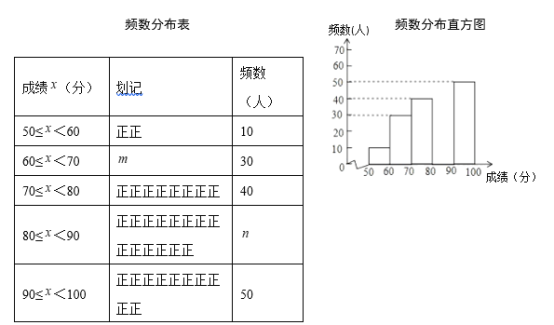
根据所给信息,解答下列问题:
(1)在这个问题中,有以下说法:①2800名学生是总体;②200名学生的成绩是总体的一个样本;③每名学生是总体的一个个体;④样本容量是200;⑤以上调查是全面调查.其中正确的说法是 (填序号)
(2) 统计表中m= ,n= ;
(3) 补全频数分布直方图;
(4) 若成绩在90分以上(包括90分)为优等,请你估计该校参加本次比赛的2800名学生中成绩是优等的约为多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com