
【题目】如图,在平面直角坐标系中,已知△ABC,点A的坐标是(4,0),点B的坐标是(2,3),点C在x轴的负半轴上,且AC=6.
(1)直接写出点C的坐标.
(2)在y轴上是否存在点P,使得S△POB=![]() S△ABC若存在,求出点P的坐标;若不存在,请说明理由.
S△ABC若存在,求出点P的坐标;若不存在,请说明理由.
(3)把点C往上平移3个单位得到点H,作射线CH,连接BH,点M在射线CH上运动(不与点C、H重合).试探究∠HBM,∠BMA,∠MAC之间的数量关系,并证明你的结论.

【答案】(1)C(-2,0);(2)点P坐标为(0,6)或(0,-6);(3)∠BMA=∠MAC±∠HBM,证明见解析.
【解析】
(1)由点A坐标可得OA=4,再根据C点x轴负半轴上,AC=6即可求得答案;
(2)先求出S△ABC=9,S△BOP=OP,再根据S△POB=![]() S△ABC,可得OP=6,即可写出点P的坐标;
S△ABC,可得OP=6,即可写出点P的坐标;
(3)先得到点H的坐标,再结合点B的坐标可得到BH//AC,然后根据点M在射线CH上,分点M在线段CH上与不在线段CH上两种情况分别进行讨论即可得.
(1)∵A(4,0),
∴OA=4,
∵C点x轴负半轴上,AC=6,
∴OC=AC-OA=2,
∴C(-2,0);
(2)∵B(2,3),
∴S△ABC=![]() ×6×3=9,S△BOP=
×6×3=9,S△BOP=![]() OP×2=OP,
OP×2=OP,
又∵S△POB=![]() S△ABC,
S△ABC,
∴OP=![]() ×9=6,
×9=6,
∴点P坐标为(0,6)或(0,-6);
(3)∠BMA=∠MAC±∠HBM,证明如下:
∵把点C往上平移3个单位得到点H,C(-2,0),
∴H(-2,3),
又∵B(2,3),
∴BH//AC;
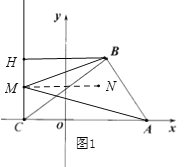
如图1,当点M在线段HC上时,过点M作MN//AC,
∴∠MAC=∠AMN,MN//HB,
∴∠HBM=∠BMN,
∵∠BMA=∠BMN+∠AMN,
∴∠BMA=∠HBM+∠MAC;
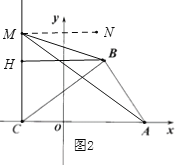
如图2,当点M在射线CH上但不在线段HC上时,过点M作MN//AC,
∴∠MAC=∠AMN,MN//HB,
∴∠HBM=∠BMN,
∵∠BMA=∠AMN-∠BMN,
∴∠BMA=∠MAC-∠HBM;
综上,∠BMA=∠MAC±∠HBM.


科目:初中数学 来源: 题型:
【题目】已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,点Q也停止移动,如图②.设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.解答下列问题:

(1)当t为何值时,PQ∥AB?
(2)当t=3时,求△QMC的面积;
(3)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宜昌四中男子篮球队在2016全区篮球比赛中蝉联冠军,让全校师生倍受鼓舞.在一次与第25中学的比赛中,运动员小涛在距篮下4米处跳起投篮,如图所示,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的直角坐标系,求抛物线的表达式;
(2)运动员小涛的身高是1.8米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,小涛跳离地面的高度是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )

A. 函数有最小值
B. 对称轴是直线x=![]()
C. 当x<![]() ,y随x的增大而减小
,y随x的增大而减小
D. 当﹣1<x<2时,y>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把二次函数y=a(x-h)2+k的图象先向左平移2个单位,再向上平移4个单位,得到二次函数y=![]() (x+1)2-1的图象.
(x+1)2-1的图象.
(1)试确定a,h,k的值;
(2)指出二次函数y=a(x-h)2+k的开口方向,对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年2月初,在抵御新冠肺炎的工作中,全国各地口罩严重供应不足,某乡镇企业缝纫车间立即转岗做口罩以供应本地志愿者和卫生系统,该车间有技术工人15人,生产部为了合理制定口罩的日生产定额,统计了15人某天加工口罩数如下:
车间15名工人某一天加工口罩个数统计表
加工零件数/个 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)求这一天15名工人加工口罩数的平均数、中位数和众数.
(2)为了提高大多数工人的积极性,管理者准备试行“每天定额生产,超产有奖”的措施,假如你是管理者,从平均数、中位数、众数的角度进行分析,你将如何确定这个“定额”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1) 如图1,正方形ABCD的边长为5,点E是AB上一点,点F是AD延长线上一点,且BE=DF,四边形AEGF是矩形,写出矩形AEGF的面积y与BE的长x之间的函数关系式;
(2) 如图2,已知一长方形打印纸长20 cm,宽15 cm,现在要在打印纸上打印文稿,上下左右各留出一定距离.设留出的距离均为x cm,打印文稿面积为y cm2,试写出y与x之间的关系式,并求出x的取值范围.
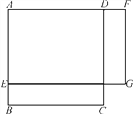
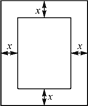
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班为了从甲、乙两同学中选出班长,进行了一次演讲答辩与民主测评.A、B、C、D、E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了民主测评.结果如下表所示:
表1 演讲答辩得分表(单位:分)
A | B | C | D | E | |
甲 | 90 | 92 | 94 | 95 | 88 |
乙 | 89 | 86 | 87 | 94 | 91 |
表2 民主测评票数统计表(单位:张)
“好”票数 | “较好”票数 | “一般”票数 | |
甲 | 40 | 7 | 3 |
乙 | 42 | 4 | 4 |
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;
民主测评得分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;
综合得分=演讲答辩得分×(1﹣a)+民主测评得分×a(0.5≤a≤0.8).
(1)当a=0.6时,甲的综合得分是多少?
(2)a在什么范围时,甲的综合得分高?a在什么范围时,乙的综合得分高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com