
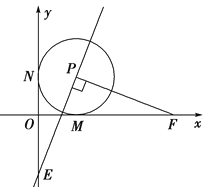
【题目】已知O是坐标原点,以P(1,1)为圆心的⊙P与x轴、y轴分别相切于点M和点N.点F从点M出发,沿x轴正方向以每秒1个单位长度的速度运动,连结PF,过点P作PE⊥PF交y轴于点E.设点F运动的时间是t秒(t>0).
(1)求点E的坐标(用t表示);
(2)在点F运动过程中,当PF=2OE时,求t的值.
(3)当t>1时,作点F关于点M的对称点F′.点Q是线段MF′的中点,连结QE.在点F运动过程中,是否存在某一时刻,使得△QOE与△PMF相似,若存在,求出t的值;若不存在,请说明理由.
【答案】(1)E(0,1-t);(2)![]() 或
或![]() ;(3)存在:当t=
;(3)存在:当t=![]() ,t=
,t=![]() ,t=2+
,t=2+![]() 时,使得△QOE与△PMF相似.
时,使得△QOE与△PMF相似.
【解析】试题分析:
(1)连接PM、PN,由已知条件易证△PMF≌△PNE,由此可得NE=MF=t,则可得OE=t-1,结合点E在y轴的负半轴即可得到点E的坐标了;
(2)在Rt△PFM中,易得PF=![]() ,结合OE=
,结合OE=![]() 即可得到方程
即可得到方程![]() ,解此方程即可求得对应的t的值;
,解此方程即可求得对应的t的值;
(3)由F(1+t,0),F和F′关于点M对称可得F′(1-t,0),结合点Q是线段MF′的中点可得Q(1-![]() t,0),然后在1<t<2时,分△OEQ∽△MPF和△OEQ∽△MFP两种情况讨论计算可求得对应的t的值;在当t>2时,分△OEQ ∽△MPF和△OEQ ∽△MFP两种情况讨论计算可求得对应的t的值.
t,0),然后在1<t<2时,分△OEQ∽△MPF和△OEQ∽△MFP两种情况讨论计算可求得对应的t的值;在当t>2时,分△OEQ ∽△MPF和△OEQ ∽△MFP两种情况讨论计算可求得对应的t的值.
试题解析:
(1)如下图,连结PM,PN.
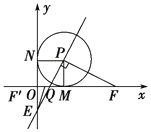
∵以P(1,1)为圆心的⊙P与x轴、y轴分别相切于点M和点N,
∴∠PNE=∠PMF=∠MPN=90°,
∴∠NPE+∠EPM=∠EPM+∠MPF=90°,
∴∠NPE=∠MPF,
又∵PM=PN,
∴△PMF≌△PNE,
∴NE=MF=t,
∴OE=t-1,
∴E(0,1-t);
(2)在直角△PMF中![]() ,
, ![]() ,
,
由PF=2OE得![]()
![]() ,
,
解得![]() 或
或![]() .
.
(3)存在,理由如下;
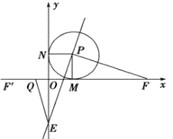
∵F(1+t,0),F和F′关于点M对称,
∴F′(1-t,0),
∵点Q是MF′的中点,
∴Q(1-![]() t,0),
t,0),
①当1<t<2时,如图,有OQ=1-![]() t,
t,
由(1)得∴NE=MF=t,OE=t-1.
当△OEQ∽△MPF时,
∴![]() ,
,
∴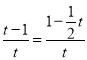 ,
,
解得,t=![]() 或t=
或t=![]() (舍去);
(舍去);
当△OEQ∽△MFP时, ![]() ,
,
∴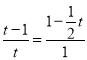 ,解得,t=
,解得,t=![]() 或t=
或t=![]() (舍去);
(舍去);
②当t>2时,如图,有OQ=![]() t-1,
t-1,
由(1)得NE=MF=t,OE=t-1,
当△OEQ ∽△MPF, ![]() ,
,
∴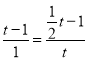 ,无解;
,无解;
当△OEQ ∽△MFP时, ![]() ;
;
∴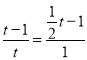 ,
,
解得![]() 或
或![]() (舍去).
(舍去).
综上所述,当t=![]() ,t=
,t=![]() ,
, ![]() 时,使得△QOE与△PMF相似.
时,使得△QOE与△PMF相似.


 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源: 题型:
【题目】典典同学学完统计知识后,随机调查了她家所在辖区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图:
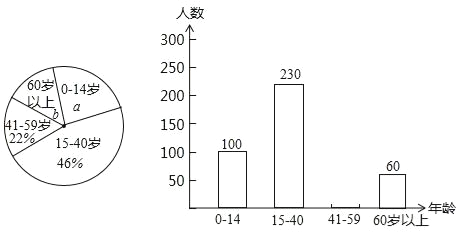
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)扇形统计图中a= ,b= ;并补全条形统计图;
(2)若该辖区共有居民3500人,请估计年龄在0~14岁的居民的人数.
(3)一天,典典知道了辖区内60岁以上的部分老人参加了市级门球比赛,比赛的老人们分成甲、乙两组,典典很想知道甲乙两组的比赛结果,王大爷告诉说,甲组与乙组的得分和为110,甲组得分不低于乙组得分的1.5倍,甲组得分最少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.
例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
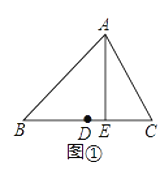
(1)设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是________,推断的数学依据是________.
(2)如图②,在△ABC中,∠B=45°,AB=![]() ,BC=8,AD为边BC的中线,求边BC的中垂距.
,BC=8,AD为边BC的中线,求边BC的中垂距.

(3)如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念李时珍诞辰500周年,蕲春县投巨资建设如图所示展览馆,其外框是一个大正方形,中间四个大小相同的正方形(阴影部分)是支展馆的核心筒,标记了字母的五个大小相同的正方形是展厅,剩余的四个大小相同的图形是休息厅,已知核心筒的正方形边长比展厅的正方形边长的一半多1米
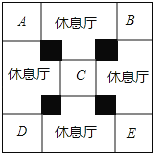
(1)若设展厅的正方形边长为a米,则用含a的代数式表示核心筒的正方形边长为 米.
(2)若设核心筒的正方形边长为b米,求该展馆外框大正方形的周长(用含b的代数式表示).
(3)若展览馆外框大正形边长为26米,求休息厅的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
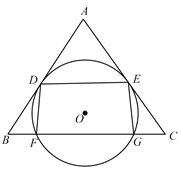
【题目】如图, ![]() 是
是 ![]() 内一点,
内一点, ![]() 与
与 ![]() 相交于
相交于 ![]() 、
、![]() 两点,且与
两点,且与 ![]() 、
、![]() 分别相切于点
分别相切于点 ![]() 、
、![]() ,
, ![]() .连接
.连接 ![]() 、
、![]() .
.
(1)求证: ![]() .
.
(2)已知 ![]() ,
, ![]() .求四边形
.求四边形 ![]() 是矩形时
是矩形时 ![]() 的半径.
的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与y轴正半轴相交,其顶点坐标为(
的图象与y轴正半轴相交,其顶点坐标为(![]() ,1),下列结论:①abc>0;②a=b;③a=4c﹣4;④方程
,1),下列结论:①abc>0;②a=b;③a=4c﹣4;④方程![]() 有两个相等的实数根,其中正确的结论是______.(只填序号即可).
有两个相等的实数根,其中正确的结论是______.(只填序号即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】轮船沿江从A港顺流行驶到B港,比从B港返回A港少用3小时,若船速为26千米/时,水速为2千米/时,求A港和B港相距多少千米.设A港和B港相距x千米.根据题意,可列出的方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A,B,C的位置如图,点C是线段AB的中点,点A表示的数比点C表示的数的两倍还大3,点B和点C表示的数是互为相反数,点C表示的数是__________.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com