
 的坐标为(1,0).将线段
的坐标为(1,0).将线段 绕原点O沿逆时针方向旋转45
绕原点O沿逆时针方向旋转45 ,再将其延长到
,再将其延长到 ,使得
,使得 ,得到线段
,得到线段 ;又将线段
;又将线段 绕原点O沿逆时针方向旋转45
绕原点O沿逆时针方向旋转45 ,再将其延长到
,再将其延长到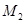 ,使得
,使得 ,得到线段
,得到线段 ,如此下去,得到线段
,如此下去,得到线段 ,
, ,…,
,…, .
.
 的周长;
的周长; (
( 0,1,2,3…)的横坐标
0,1,2,3…)的横坐标 ,纵坐标
,纵坐标 都取绝对值后得到的新坐标
都取绝对值后得到的新坐标 称之为点
称之为点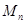 的“绝对坐标”.根据图中点
的“绝对坐标”.根据图中点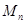 的分布规律,请写出点
的分布规律,请写出点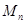 的“绝对坐标”.
的“绝对坐标”. 的周长是
的周长是 (3)①当
(3)①当 时(其中
时(其中 =0,1,2,3,…),点在
=0,1,2,3,…),点在 轴上,则
轴上,则 (
( )
)  时(其中
时(其中 =1,2,3,…),点在
=1,2,3,…),点在 轴上,点
轴上,点 (
( )
)  =1,2,3,…,时,点在各象限的分角线上,则点
=1,2,3,…,时,点在各象限的分角线上,则点 (
( )
) ,
, ,
,
 的周长是
的周长是
 旋转8次之后回到
旋转8次之后回到 轴的正半轴,在这8次旋转中,点
轴的正半轴,在这8次旋转中,点 分别落在坐标象限的分角线上或
分别落在坐标象限的分角线上或 轴或
轴或 轴上,但各点“绝对坐标”的横、纵坐标均为非负数,因此,点
轴上,但各点“绝对坐标”的横、纵坐标均为非负数,因此,点 的“绝对坐标”可分三类情况:
的“绝对坐标”可分三类情况:
 ),M4(
),M4( ),M8(
),M8( ),M12(
),M12( ),…,
),…, 的“绝对坐标”为(
的“绝对坐标”为( )。
)。  ,M6
,M6 ,M10
,M10 ,M14
,M14 ,……,
,……, 的“绝对坐标”为
的“绝对坐标”为 .
.  ,M3
,M3 ,M5
,M5 ,M7
,M7 ,即:
,即: 的“绝对坐标”为
的“绝对坐标”为 .
.  旋转8次之后回到
旋转8次之后回到 轴的正半轴,在这8次旋转中,点分别落在坐标象限的分角线上或
轴的正半轴,在这8次旋转中,点分别落在坐标象限的分角线上或 轴或
轴或 轴上,但各点“绝对坐标”的横、纵坐标均为非负数,因此,各点的“绝对坐标”可分三种情况:
轴上,但各点“绝对坐标”的横、纵坐标均为非负数,因此,各点的“绝对坐标”可分三种情况: 时(其中
时(其中 =0,1,2,3,…),点在
=0,1,2,3,…),点在 轴上,则
轴上,则 (
( )
)  时(其中
时(其中 =1,2,3,…),点在
=1,2,3,…),点在 轴上,点
轴上,点 (
( )
)  =1,2,3,…,时,点在各象限的分角线上,则点
=1,2,3,…,时,点在各象限的分角线上,则点 (
( )
) 

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,
中, ,
, ,将一块等腰直角三角板的直角顶点放在斜边
,将一块等腰直角三角板的直角顶点放在斜边 的中点
的中点 处,将三角板绕点
处,将三角板绕点 旋转,三角板的两直角边分别交射线
旋转,三角板的两直角边分别交射线 、
、 于
于 、
、 两点. 如图①、②、③是旋转三角板得到的图形中的三种情况,试探究:
两点. 如图①、②、③是旋转三角板得到的图形中的三种情况,试探究:
 旋转,观察线段
旋转,观察线段 和
和 之间有什么数量关系?并结合图②加以证明;
之间有什么数量关系?并结合图②加以证明; 旋转,
旋转, 是否能成为等腰三角形?若能,写出所有
是否能成为等腰三角形?若能,写出所有 为等腰三角形时
为等腰三角形时 的长(直接写出答案即可);若不能,请说明理由;
的长(直接写出答案即可);若不能,请说明理由; ,若将三角板的直角顶点放在斜边
,若将三角板的直角顶点放在斜边 上的
上的 处,且
处,且 ,和前面一样操作,试问线段
,和前面一样操作,试问线段 和
和 之间有什么数量关系?并结合图④证明你的结论.
之间有什么数量关系?并结合图④证明你的结论.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.40° | B.50° | C.60° | D.70° |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com