



科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 、
、 为它的对角线,E为AB边上一动点(点E不与点A、B重合),EF∥AC交BC于点F,FG∥BD交DC于点G,GH∥AC交AD于点H,连接HE.记四边形EFGH的周长为
为它的对角线,E为AB边上一动点(点E不与点A、B重合),EF∥AC交BC于点F,FG∥BD交DC于点G,GH∥AC交AD于点H,连接HE.记四边形EFGH的周长为 ,如果在点
,如果在点 的运动过程中,
的运动过程中, 的值不变,则我们称四边形ABCD为“
的值不变,则我们称四边形ABCD为“ 四边形”, 此时
四边形”, 此时 的值称为它的“
的值称为它的“ 值”.经过探究,可得矩形是“
值”.经过探究,可得矩形是“ 四边形”.如图2,矩形ABCD中,若AB=4,BC=3,则它的“
四边形”.如图2,矩形ABCD中,若AB=4,BC=3,则它的“ 值”为 .
值”为 .
 四边形”;
四边形”; 是⊙O的直径,A是⊙O上一点,
是⊙O的直径,A是⊙O上一点, ,点
,点 为
为 上的一动点,将△
上的一动点,将△ 沿
沿 的中垂线翻折,得到△
的中垂线翻折,得到△ .当点
.当点 运动到某一位置时,以
运动到某一位置时,以 、
、 、
、 、
、 、
、 、
、 中的任意四个点为顶点的“
中的任意四个点为顶点的“ 四边形”最多,最多有 个.
四边形”最多,最多有 个.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的坐标为(1,0).将线段
的坐标为(1,0).将线段 绕原点O沿逆时针方向旋转45
绕原点O沿逆时针方向旋转45 ,再将其延长到
,再将其延长到 ,使得
,使得 ,得到线段
,得到线段 ;又将线段
;又将线段 绕原点O沿逆时针方向旋转45
绕原点O沿逆时针方向旋转45 ,再将其延长到
,再将其延长到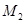 ,使得
,使得 ,得到线段
,得到线段 ,如此下去,得到线段
,如此下去,得到线段 ,
, ,…,
,…, .
.
 的周长;
的周长; (
( 0,1,2,3…)的横坐标
0,1,2,3…)的横坐标 ,纵坐标
,纵坐标 都取绝对值后得到的新坐标
都取绝对值后得到的新坐标 称之为点
称之为点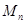 的“绝对坐标”.根据图中点
的“绝对坐标”.根据图中点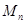 的分布规律,请写出点
的分布规律,请写出点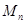 的“绝对坐标”.
的“绝对坐标”.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com