
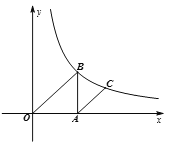
【题目】如图,在平面直角坐标系xOy中,已知点A的坐标为(a,0)(其中a>0),作AB∥y轴交反比例函数![]() (k>0,x>0)的图象于点B.
(k>0,x>0)的图象于点B.
(1)当△OAB的面积为2时,①求k的值;②若a=2,过A点作AC∥OB交![]() (k>0,x>0)图象于点C,求C的横坐标;
(k>0,x>0)图象于点C,求C的横坐标;
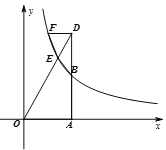
(2)若D为射线AB上一点,连接OD交反比例函数图象于点E,DF∥x轴交反比例函数![]() (k>0,x>0)的图象于点F,连接EF、EB,试猜想:
(k>0,x>0)的图象于点F,连接EF、EB,试猜想:![]() 的值是否随a的变化而变化?如果不变,求出
的值是否随a的变化而变化?如果不变,求出![]() 的值;如果变化,请说明理由.
的值;如果变化,请说明理由.
【答案】(1)①4;②点C横坐标为![]() ;(2) 不变,比值为1.
;(2) 不变,比值为1.
【解析】(1)①由B(a,![]() ),得到OA=a,AB=
),得到OA=a,AB=![]() , 由S△OAB=
, 由S△OAB=![]() ·AB·OA=2,即可得到结论;
·AB·OA=2,即可得到结论;
②过点C作CD⊥AO于点D,得到B(2,2),设AD=b,则C(2+b,![]() ),可证△OAB∽△ADC,得到
),可证△OAB∽△ADC,得到![]() ,即
,即![]() ,解方程得到b的值,从而得到点C的横坐标.
,解方程得到b的值,从而得到点C的横坐标.
(2)不变,比值为1.设![]() ,则yOE=
,则yOE=![]() ,由S△DBE=
,由S△DBE=![]()
![]() ,S△DEF=
,S△DEF=![]() ,代入
,代入![]()
![]() 化简即可得到结论.
化简即可得到结论.
(1)①∵B(a,![]() ),∴OA=a,AB=
),∴OA=a,AB=![]() , ∴S△OAB=
, ∴S△OAB=![]() ·AB·OA=2,∴k=4;
·AB·OA=2,∴k=4;
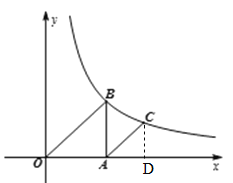
②过点C作CD⊥AO于点D.
∵a=2,∴B(2,2),
设AD=b,∴C(2+b,![]() ).
).
∵AC∥OB,∴∠BOA=∠CAD.
∵∠BAO=∠CDA,∴△OAB∽△ADC,
∴![]() ,∴
,∴![]() ,∴b=
,∴b=![]() ,解得:b=-1+
,解得:b=-1+![]() (负值舍去),∴点C的横坐标=2-1+
(负值舍去),∴点C的横坐标=2-1+![]() =
=![]() .
.
(2)不变,比值为1.理由如下:
设![]() yOE=
yOE=![]() ∴
∴![]() .
.
∵S△DBE=![]()
![]() ,S△DEF=
,S△DEF=![]()
∴![]() =
=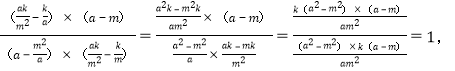 ∴
∴![]() =1.
=1.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
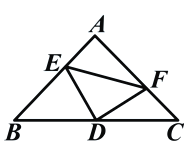
【题目】如图,已知△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线,交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:BD=CD;(2)如果AB=AC,试判断四边形AFBD的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区商店以2元的批发价进了一批纪念品.经调查发现,每个定价3元,每天可以能卖出500件,而且定价每上涨0.1元,其销售量将减少10件.根据规定:纪念品售价不能超过批发价的2.5倍.
(1)当每个纪念品定价为3.5元时,商店每天能卖出________件;
(2)如果商店要实现每天800元的销售利润,那该如何定价?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人同时从相距25千米的A地去B地,甲骑摩托车,乙骑自行车,甲的速度是乙的速度的3倍,甲到达B地后停留了30分钟,然后从B地返回A地,在途中遇见了乙,此时距他们出发的时间刚好是1小时,则甲的速度是( )
A. 20千米/小时 B. 60千米/小时
C. 25千米/小时 D. 75千米小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等,经洽谈,甲商场优惠方案是:每购买十套队服,送一个足球;乙商场优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)求每套队服和每个足球的价格是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用;
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.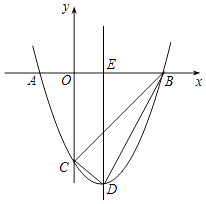
(1)求证△BCD是直角三角形;
(2)点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在等腰直角三角形中,AB=AC,点D是斜边BC上的中点,点E、F分别为AB,AC上的点,且DE⊥DF。(1)若设![]() ,
,![]() ,满足
,满足![]() .
.
(1)求BE及CF的长。
(2)求证:![]() 。
。
(3)在(1)的条件下,求△DEF的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com