
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.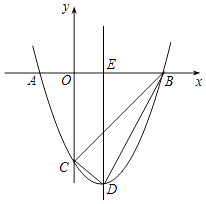
(1)求证△BCD是直角三角形;
(2)点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.
【答案】
(1)
解:把A(﹣1,0)和B(3,0)两点代入抛物线y=x2+bx+c中得:
![]() ,
,
解得: ![]() ,
,
∴抛物线的解析式为:y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴C(0,﹣3),D(1,﹣4),
由勾股定理得:BC2=32+32=18,
CD2=12+(4﹣3)2=2,
BD2=(3﹣1)2+42=20,
∴CD2+BC2=BD2,
即∠BCD=90°,
∴△BCD是直角三角形
(2)
解:作PQ⊥OC于点Q,
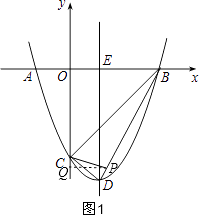
∴∠PQC=90°,
∵∠PCO+∠CDB=180°,
∠PCO+∠PCQ=180°,
∴∠CDB=∠PCQ,
∵∠PQC=∠BCD=90°,
∴△PCQ∽△BDC,
∴ ![]() =3,
=3,
∴PQ=3CQ,
设CQ=m,则PQ=3m,
设P(3m,﹣3﹣m),
设直线BD的解析式为:y=kx+b,
把B(3,0)、D(1,﹣4)代入得: ![]() ,
,
解得: ![]() ,
,
∴直线BD的解析式为:y=2x﹣6,
将点P的坐标代入直线BD:y=2x﹣6得:
﹣3﹣m=2×3m﹣6,
m= ![]() ,
,
∴3m= ![]() ,﹣3﹣m=﹣3﹣
,﹣3﹣m=﹣3﹣ ![]() =﹣
=﹣ ![]() ,
,
∴P( ![]() ,﹣
,﹣ ![]() );
);
(3)
解:∵∠CMN=∠BDE,
∴tan∠BDE=tan∠CMN= ![]() =
= ![]() ,
,
∴ ![]() ,
,
同理可求得:CD的解析式为:y=﹣x﹣3,
设N(a,﹣a﹣3),M(x,x2﹣2x﹣3),
①如图2,过N作GF∥y轴,过M作MG⊥GF于G,过C作CF⊥GF于F,
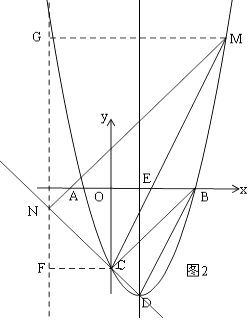
则△MGN∽△NFC,
∴ ![]() =
= ![]() ,
,
∴ ![]() =2,
=2,
则 ![]() ,
,
∴x1=0(舍),x2=5,
当x=5时,x2﹣2x﹣3=12,
∴M(5,12),
②如图3,过N作FG∥x轴,交y轴于F,过M作MG⊥GF于G,
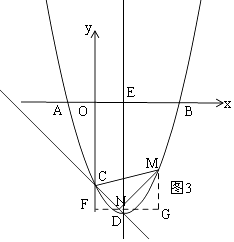
∴△CFN∽△NGM,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
则 ![]() ,
,
∴x1=0(舍),x2= ![]() ,
,
当x= ![]() 时,y=x2﹣2x﹣3=﹣
时,y=x2﹣2x﹣3=﹣ ![]() ,
,
∴M( ![]() ,﹣
,﹣ ![]() ),
),
综上所述,点M的坐标(5,12)或( ![]() ,﹣
,﹣ ![]() ).
).
【解析】(1)先利用待定系数法求二次函数的解析式,并配方成顶点式求顶点D的坐标,和与y轴的交点C的坐标,由勾股定理计算△BDC三边的平方,利用勾股定理的逆定理证明△BCD是直角三角形;(2)作辅助线,构建直角三角形PCQ与直角三角形BDC相似,根据比例式表示出点P的坐标,利用待定系数法求直线BD的解析式,因为点P为线段BD上一点,代入直线BD的解析式列方程可求出点P的坐标;(3)同理求直线CD的解析式为:y=﹣x﹣3,由此表示点N的坐标为(a,﹣a﹣3),因为M在抛物线上,所以设M(x,x2﹣2x﹣3),根据同角的三角函数得:tan∠BDE=tan∠CMN= ![]() ,则
,则 ![]() ,
,
如图2,证明△MGN∽△NFC,列比例式可得方程组解出即可;
如图3,证明△CFN∽△NGM,列比例式可得方程组解出即可.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.


科目:初中数学 来源: 题型:
【题目】如图,点A、B在线段EF上,点M、N分别是线段EA、BF的中点,EA:AB:BF=1:2:3,若MN=8cm,则线段EF的长是( )
![]()
A. 10 cm B. 11 cm C. 12 cm D. 13 cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
![]()
(1)写出数轴上A、B两点表示的数;
(2)动点P、Q分别从A、C同时出发,点P以每秒2个单位长度的速度沿数轴向右匀速运动,点Q以每秒1个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒,t为何值时,原点O、与P、Q三点中,有一点恰好是另两点所连线段的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
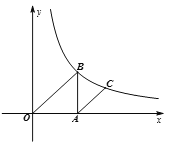
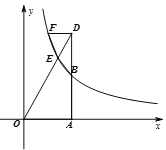
【题目】如图,在平面直角坐标系xOy中,已知点A的坐标为(a,0)(其中a>0),作AB∥y轴交反比例函数![]() (k>0,x>0)的图象于点B.
(k>0,x>0)的图象于点B.
(1)当△OAB的面积为2时,①求k的值;②若a=2,过A点作AC∥OB交![]() (k>0,x>0)图象于点C,求C的横坐标;
(k>0,x>0)图象于点C,求C的横坐标;
(2)若D为射线AB上一点,连接OD交反比例函数图象于点E,DF∥x轴交反比例函数![]() (k>0,x>0)的图象于点F,连接EF、EB,试猜想:
(k>0,x>0)的图象于点F,连接EF、EB,试猜想:![]() 的值是否随a的变化而变化?如果不变,求出
的值是否随a的变化而变化?如果不变,求出![]() 的值;如果变化,请说明理由.
的值;如果变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
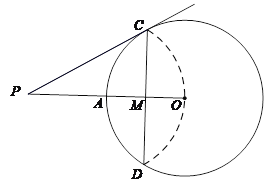
【题目】如图,已知⊙O的半径为4,OA为半径,CD为弦,OA与CD交于点M,将弧CD沿着CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC.
(1)求CD的长;
(2)求证:PC是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
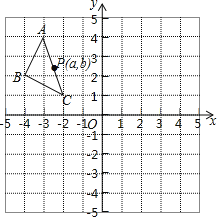
【题目】如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(-3,4),B(-4,2),C(-2,1),且△A1B1C1与△ABC关于原点O成中心对称。
(1)画出△A1B1C1,并写出点A1的坐标;
(2)P(a,b)是△ABC的AC边上一点,△ABC经平移后点P的对应点为P'(a+3,b+1),请画出平移后的△A2B2C2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于点D,下列四个结论:
①EF=BE+CF;
②∠BOC=90°+![]() ∠A;
∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是( )
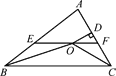
A. ①②③ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将连续的奇数1、3、5、7、9,……排成如下的数表:
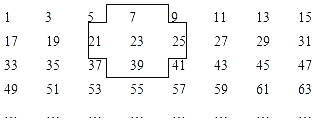
(1)十字框中的5个数的和与中间的数23有什么关系?若将十字框上下左右平移,可框住另外5个数,这5个数还有这种规律吗?
(2)设十字框中中间的数为a,用含a的式子表示十字框中的其他四个数;
(3)十字框中的5个数的和能等于2018吗?若能,请写出这5个数;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识是用来为人类服务的,我们应该把它们用于有意义的方面.下面就两个情景请你作出评判.
情景一:从教室到图书馆,总有少数同学不走人行道而横穿草坪,这是为什么呢?试用所学数学知识来说明这个问题.

情景二:A、B是河流l两旁的两个村庄,现要在河边修一个抽水站向两村供水,问抽水站修在什么地方才能使所需的管道最短?请在图中表示出抽水站点P的位置,并说明你的理由:

你赞同以上哪种做法?你认为应用数学知识为人类服务时应注意什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com