
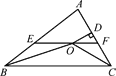
【题目】如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于点D,下列四个结论:
①EF=BE+CF;
②∠BOC=90°+![]() ∠A;
∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是( )
A. ①②③ B. ①②④ C. ②③④ D. ①③④
【答案】A
【解析】由在△ABC中,∠ABC和∠ACB的平分线相交于点O,根据角平分线的定义与三角形内角和定理,即可求得②∠BOC=90°+![]() ∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF=BE+CF故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故③正确;由角平分线定理与三角形面积的求解方法,即可求得③设OD=m,AE+AF=n,则S△AEF=
∠A正确;由平行线的性质和角平分线的定义得出△BEO和△CFO是等腰三角形得出EF=BE+CF故①正确;由角平分线的性质得出点O到△ABC各边的距离相等,故③正确;由角平分线定理与三角形面积的求解方法,即可求得③设OD=m,AE+AF=n,则S△AEF=![]() mn,故④错误.
mn,故④错误.
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,∠A+∠ABC+∠ACB=180°,
∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°-![]() ∠A,
∠A,
∴∠BOC=180°-(∠OBC+∠OCB)=90°+![]() ∠A;故②正确;
∠A;故②正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,
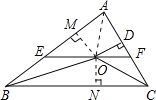
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,
∴S△AEF=S△AOE+S△AOF=![]() AEOM+
AEOM+![]() AFOD=
AFOD=![]() OD(AE+AF)=
OD(AE+AF)=![]() mn;故④错误;
mn;故④错误;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴点O到△ABC各边的距离相等,故③正确.
故选:A.


科目:初中数学 来源: 题型:
【题目】甲、乙两家超市进行促销活动,甲超市采用“买100减50”的促销方式,即购买商品的总金额满100元但不足200元,少付50元;满200元但不足300元,少付100元;….乙超市采用“打6折”的促销方式,即顾客购买商品的总金额打6折.
(1)若顾客在甲商场购买商品的总金额为x(100≤x<200)元,优惠后得到商家的优惠率为p(p= ![]() ),写出p与x之间的函数关系式,并说明p随x的变化情况;
),写出p与x之间的函数关系式,并说明p随x的变化情况;
(2)王强同学认为:如果顾客购买商品的总金额超过100元,实际上甲超市采用“打5折”、乙超市采用“打6折”,那么当然选择甲超市购物.请你举例反驳;
(3)品牌、质量、规格等都相同的某种商品,在甲乙两商场的标价都是x(300≤x<400)元,认为选择哪家商场购买商品花钱较少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人同时从相距25千米的A地去B地,甲骑摩托车,乙骑自行车,甲的速度是乙的速度的3倍,甲到达B地后停留了30分钟,然后从B地返回A地,在途中遇见了乙,此时距他们出发的时间刚好是1小时,则甲的速度是( )
A. 20千米/小时 B. 60千米/小时
C. 25千米/小时 D. 75千米小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.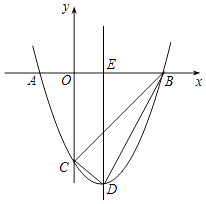
(1)求证△BCD是直角三角形;
(2)点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)若AD=5,BD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OC是∠AOB内的一条射线,OD、OE分别平分∠AOB、∠AOC.
(1)若∠AOC=20°,∠AOB=110°,则∠BOC= °,∠DOE= °;
(2)若∠AOC=m°,∠AOB=n°(n>m),则∠BOC= °,∠DOE= °;
(3)猜想:∠DOE与∠BOC有怎样的数量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(0<t≤15).过点D作DF⊥BC于点F,连接DE,EF.

(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值,如果不能,说明理由;
(3)当t为何值时,△DEF为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=4,AO=BO,P是射线CO上的一个动点,∠AOC=60°,则当△PAB为直角三角形时,AP的长为 __________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com