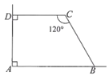
【题目】如图，利用一个直角墙角修建一个梯形储料场ABCD，其中∠C＝120°．若新建墙BC与CD总长为12m，则该梯形储料场ABCD的最大面积是（ ）
A.18m2B.
m2C.
m2D.
m2
【答案】C
【解析】
过点C作CE⊥AB于E，则四边形ADCE为矩形，CD=AE=x，∠DCE=∠CEB=90°，则
∠BCE=∠BCD-∠DCE=30°，BC=12-x，由直角三角形的，性质得出
得出
，又梯形面积公式求出梯形ABCD的面积S与x之间的函数关系式，根据二次函数的性质求解.
解：如图，过点C作CE⊥AB于E，
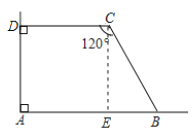
则四边形ADCE为矩形，CD=AE=x，∠DCE=∠CEB=90°，则∠BCE=∠BCD-∠DCE=30°，BC=12-x，
在Rt△CBE中，∵∠CEB=90°，
∴梯形ABCD面积
∴当x=4时，S最大=24
．
即CD长为4 m时，使梯形储料场ABCD的面积最大为24 m2；
故选：C．
科目：初中数学 来源： 题型：
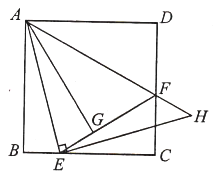
【题目】如图，已知正方形
的边长为
，
是边
上一点，
，将
，
分别沿折痕
，
向内折叠，点
，
在点
处重合，过点作
，交的延长线于
.则下列结论正确的有（ ）
①
；②
为等腰直角三角形；③点
是
的中点；④
.
A.
个B.
个C.
个D.
个
查看答案和解析>>
科目：初中数学 来源： 题型：
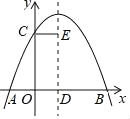
【题目】如图，抛物线y＝ax2+bx+c(a≠0)与y轴交于点C，与x轴交于A，B两点，其中点B的坐标为B(4，0)，抛物线的对称轴交x轴于点D，CE∥AB，并与抛物线的对称轴交于点E现有下列结论：①b2﹣4a＜0；②b＞0；③5a+b＜0；④AD+CE＝4．其中正确结论个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系
中，A、B为x轴上两点，C、D为y轴上的两点，经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线，我们把这条封
闭曲线称为“蛋线”．已知点C的坐标为（0，
），点M是抛物线C2：
（
＜0）的顶点．
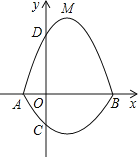
（1）求A、B两点的坐标；
（2）“蛋线”在第四象限上是否存在一点P，使得△PBC的面积最大？若存在，求出△PBC面积的最大值；若不存在，请说明理由；
（3）当△BDM为直角三角形时，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，将正方形
绕点
逆时针旋转
后得到正方形
，依此方式，绕点连续旋转2019次得到正方形
，如果点
的坐标为（1，0），那么点
的坐标为________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（1）解方程：
（2）如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，
的三个顶点坐标分别为
，
，
.
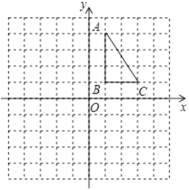
①画出关于
轴对称的
；
②画出绕点
逆时针旋转
后的
；
③在②的条件下，求线段
扫过的面积（结果保留
）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】 如图，直线
交
轴于点
，交
轴于点
，抛物线
经过点，交轴于点
．点
为抛物线上一动点，过点作轴的垂线，交直线
于点
，设点的横坐标为
．
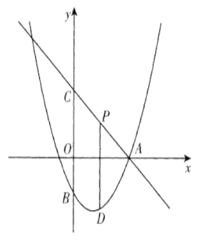
（1）求抛物线的解析式；
（2）当点在直线下方的抛物线上运动时，求线段
长度的最大值；
（3）若点
是平面内任意一点，是否存在点，使以
，，，为顶点的四边形为菱形？若存在，请直接出的值；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学课外兴趣活动小组准备围建一个矩形花草园，其中一边靠墙，另外三边周长为30米的篱笆围成．已知墙长为16米（如图所示），设这个花草园垂直于墙的一边长为x米．
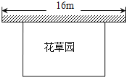
(1)若花草园的面积为100平方米，求x；
(2)若平行于墙的一边长不小于10米，这个花草园的面积有最大值和最小值吗？如果有，求出最大值和最小值；如果没有，请说明理由；
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
