
【题目】 如图,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,交
,交![]() 轴于点
轴于点![]() .点
.点![]() 为抛物线上一动点,过点
为抛物线上一动点,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
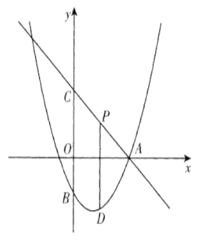
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 下方的抛物线上运动时,求线段
下方的抛物线上运动时,求线段![]() 长度的最大值;
长度的最大值;
(3)若点![]() 是平面内任意一点,是否存在点
是平面内任意一点,是否存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形?若存在,请直接出
为顶点的四边形为菱形?若存在,请直接出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,线段
时,线段![]() 的长度有最大值,为
的长度有最大值,为![]() ;(3)存在,
;(3)存在,![]() 的值为
的值为![]() ,
,![]() ,
,![]() 或
或![]() .
.
【解析】
(1)先根据直线解析式求得点A的坐标,再将点A、B的坐标代入抛物线的解析式中即可得到答案;(2)根据PD⊥x轴知点P的横坐标为m,由点D与点P所在的位置表示两点的坐标,得到线段PD的二次函数解析式,利用顶点式解析式即可求得最大值;(3)当四边形为菱形时四条边相等,故△BCP为等腰三角形,分三种情况,根据两边相等求得m值
解:(1)对于![]() ,
,
令![]() ,得
,得![]() ,
,
∴![]() .
.
将![]() ,
,![]() 代入
代入![]() ,
,
得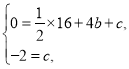
解得
故抛物线的解析式为![]() .
.
(2)易得![]() ,
,![]() ,
,
∴ ![]()
![]()
![]()
∵ 点![]() 在直线
在直线![]() 下方的抛物线上,
下方的抛物线上,
∴ ![]() .
.
∵ ![]()
∴ 当![]() 时,线段
时,线段![]() 的长度有最大值,为
的长度有最大值,为![]() .
.
(3)存在,![]() 的值为
的值为![]() ,
,![]() ,
,![]() 或
或![]() .
.
解法提示:当以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形时,
为顶点的四边形为菱形时,![]() 必为等腰三角形.
必为等腰三角形.
由![]() ,
,![]() ,
,![]() ,
,
得![]() ,
,![]() ,
,
![]() .
.
分以下三种情况讨论.
①当![]() 时,
时,![]() ,
,
即![]() ,
,
解得![]() (不合题意,舍去),
(不合题意,舍去),![]() .
.
②当![]() 时,
时,![]() ,
,
即![]() ,
,
解得![]() ,
,![]() .
.
③当![]() 时,
时,![]() ,
,
即![]() ,
,
解![]() .
.
综上可知,![]() 的值为
的值为![]() ,
,![]() ,
,![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了充分利用空间,在确定公园的设计方案时,准备利用公园的一角∠MON两边为边,用总长为16m的围栏在公园中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区城②③为矩形,而且这三块区城的面积相等.
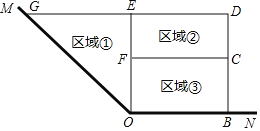
(1)设OB的长度为xm,则OE+DB的长为 m.
(2)设四边形OBDG的面积为ym2,求y与x之间的函数关系式;
(3)x为何值时,y有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的纸箱里有分别标有汉字“热”“爱”“祖”“国”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先摇匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“国”字的概率.
(2)小红从中任取球,不放回,再从中任取一球,请用树状图或列表法,求小红取出的两个球上的汉字恰好能组成“爱国”或“祖国”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一个直角墙角修建一个梯形储料场ABCD,其中∠C=120°.若新建墙BC与CD总长为12m,则该梯形储料场ABCD的最大面积是( )
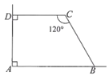
A.18m2B.![]() m2C.
m2C.![]() m2D.
m2D.![]() m2
m2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“圆材埋壁”是我国古代著名的数学著作《九章算术》中的一个问题,“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问锯几何?”用现代的数学语言表述是:“如图,CD为⊙O的直径,弦AB⊥CD垂足为E,CE=1寸,AB=10寸,求直径CD的长”,依题意,CD长为( )

A.12寸 B.13寸 C.24寸 D.26寸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E为CD上一点,若△ADE沿直线AE翻折,使点D落在BC边上点![]() 处,F为AD上一点,且
处,F为AD上一点,且![]() ,EF与BD相交于点G,
,EF与BD相交于点G,![]() 与BD相交于点H,
与BD相交于点H,![]() ,HG=2,则BD=__________.
,HG=2,则BD=__________.
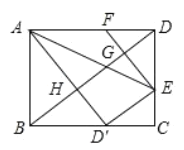
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,与
,与![]() 轴交点
轴交点![]() 在
在![]() 和
和![]() 之间(包含这两个点)运动,有如下四个结论:
之间(包含这两个点)运动,有如下四个结论:
①抛物线与![]() 轴的另一个交点是
轴的另一个交点是![]() ;
;
②点![]() ,
,![]() 在抛物线上,且满足
在抛物线上,且满足![]() ,则
,则![]() ;
;
③常数项![]() 的取值范围是
的取值范围是![]() ;
;
④系数![]() 的取值范围是
的取值范围是![]() .
.
上述结论中所有正确结论的序号是( )
A.①②③B.②③④C.①③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x+
x+![]() 与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,抛物线的对称轴与直线AC交于点E.
与x轴交于A,B两点,与y轴交于点C,点D为抛物线的顶点,抛物线的对称轴与直线AC交于点E.
(1)若点P为直线AC上方抛物线上的动点,连接PC,PE,当△PCE的面积S△PCE最大时,点P关于抛物线对称轴的对称点为点Q,此时点T从点Q开始出发,沿适当的路径运动至y轴上的点F处,再沿适当的路径运动至x轴上的点G处,最后沿适当的路径运动至直线AC上的点H处,求满足条件的点P的坐标及QF+FG+![]() AH的最小值.
AH的最小值.
(2)将△BOC绕点B顺时针旋转120°,边BO所在直线与直线AC交于点M,将抛物线沿射线CA方向平移![]() 个单位后,顶点D的对应点为D′,点R在y轴上,点N在坐标平面内,当以点D′,R,M,N为顶点的四边形是菱形时,请直接写出N点坐标.
个单位后,顶点D的对应点为D′,点R在y轴上,点N在坐标平面内,当以点D′,R,M,N为顶点的四边形是菱形时,请直接写出N点坐标.
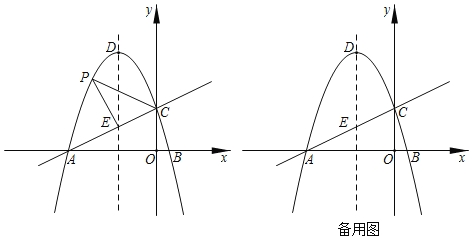
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点![]() ,
,![]() ,
,![]() .
.

(1)画出![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后的图形
后的图形![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
(2)将(1)中所得![]() 先向左平移4个单位,再向上平移2个单位得到
先向左平移4个单位,再向上平移2个单位得到![]() ,画出
,画出![]() ,并写出点
,并写出点![]() 的坐标;
的坐标;
(3)若![]() 可以看作
可以看作![]() 绕某点旋转得来,直接写出旋转中心的坐标.
绕某点旋转得来,直接写出旋转中心的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com