
【题目】为了充分利用空间,在确定公园的设计方案时,准备利用公园的一角∠MON两边为边,用总长为16m的围栏在公园中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区城②③为矩形,而且这三块区城的面积相等.
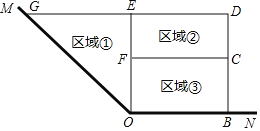
(1)设OB的长度为xm,则OE+DB的长为 m.
(2)设四边形OBDG的面积为ym2,求y与x之间的函数关系式;
(3)x为何值时,y有最大值?最大值是多少?
【答案】(1)16-3x;(2)y=﹣![]() x2+12x (0<x<
x2+12x (0<x<![]() );(3)当x=
);(3)当x=![]() 时,y有最大值,最大值是16平方米
时,y有最大值,最大值是16平方米
【解析】
(1)根据三角形和矩形的面积得到![]() EGOE=CFEF=CFOF,得到EG=DE=CF=OB=x,于是得到结论;(2)由(Ⅰ)知OE+DB=16-3x,得到OE=DB=8-1.5x,根据矩形的面积公式即可得到结论;(3)根据二次函数的性质即可得到结论.
EGOE=CFEF=CFOF,得到EG=DE=CF=OB=x,于是得到结论;(2)由(Ⅰ)知OE+DB=16-3x,得到OE=DB=8-1.5x,根据矩形的面积公式即可得到结论;(3)根据二次函数的性质即可得到结论.
解:(1)由题意得,S△OEG=S矩形CDEF=S矩形OBCF,
∴![]() EGOE=CFEF=CFOF,
EGOE=CFEF=CFOF,
∴EF=OF=![]() OE,
OE,
∴![]() EGOE=
EGOE=![]() OECF,
OECF,
∴EG=DE=CF=OB=xm,
∴OE+DB=(16﹣3x)m,
故答案为:(16﹣3x).
(2)由(1)知OE+DB=16﹣3x,
∴OE=DB=8﹣1.5x,
∴y=![]() ,
,
∵![]()
∴0<x<![]() .
.
(3)∵y=![]() ,
,
∵﹣![]() <0,且0<x<
<0,且0<x<![]() ,
,
∴抛物线开口向下
∴当x=![]() 时,y有最大值,最大值是16平方米.
时,y有最大值,最大值是16平方米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
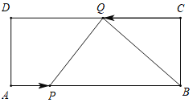
【题目】已知矩形ABCD中,AB=10,BC=4,点P从点A出发,以每秒1个单位长度沿AB方向向B运动,点Q从点C出发,以每秒2个单位长度沿CD方向向D运动,如果P、Q两点同时出发,问几秒后以△BPQ是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
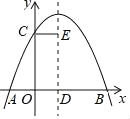
【题目】二次函数![]() 的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(
的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(![]() ,﹣2);⑤当x<
,﹣2);⑤当x<![]() 时,y随x的增大而减小;⑥a+b+c>0正确的有( )
时,y随x的增大而减小;⑥a+b+c>0正确的有( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,
,![]() 是边
是边![]() 上一点,
上一点,![]() ,将
,将![]() ,
,![]() 分别沿折痕
分别沿折痕![]() ,
,![]() 向内折叠,点
向内折叠,点![]() ,
,![]() 在点
在点![]() 处重合,过点
处重合,过点![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() .则下列结论正确的有( )
.则下列结论正确的有( )
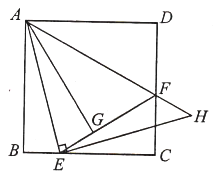
①![]() ;②
;②![]() 为等腰直角三角形;③点
为等腰直角三角形;③点![]() 是
是![]() 的中点;④
的中点;④![]() .
.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,正方形ABCD的边长为4,点E是对角线BD延长线上一点,AE=BD.将△ABE绕点A顺时针旋转α度(0°<α<360°)得到△AB′E′,点B、E的对应点分别为B′、E′.
(1)如图1,当α=30°时,求证:B′C=DE;
(2)连接B′E、DE′,当B′E=DE′时,请用图2求α的值;
(3)如图3,点P为AB的中点,点Q为线段B′E′上任意一点,试探究,在此旋转过程中,线段PQ长度的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
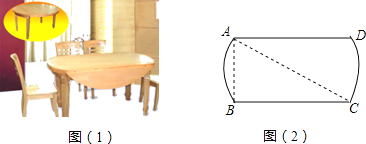
【题目】现在很多家庭都使用折叠型西餐桌来节省空间,两边翻开后成圆形桌面(如图1).餐桌两边AB和CD平行且相等(如图2),小华用皮带尺量出AC=2米,AB=1米,那么桌面翻成圆桌后,桌子面积会增加_____平方米.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
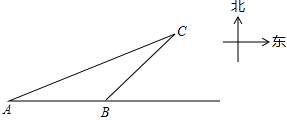
【题目】一艘轮船自西向东航行,在A处测得东偏北30°方向有一座小岛C,继续向东航行60海里到达B处,测得小岛C此时在轮船的东偏北45°方向上.之后,轮船继续向东航行多少海里,距离小岛C最近?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C,与x轴交于A,B两点,其中点B的坐标为B(4,0),抛物线的对称轴交x轴于点D,CE∥AB,并与抛物线的对称轴交于点E现有下列结论:①b2﹣4a<0;②b>0;③5a+b<0;④AD+CE=4.其中正确结论个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,交
,交![]() 轴于点
轴于点![]() .点
.点![]() 为抛物线上一动点,过点
为抛物线上一动点,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
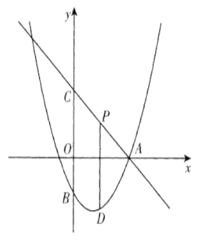
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 下方的抛物线上运动时,求线段
下方的抛物线上运动时,求线段![]() 长度的最大值;
长度的最大值;
(3)若点![]() 是平面内任意一点,是否存在点
是平面内任意一点,是否存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形?若存在,请直接出
为顶点的四边形为菱形?若存在,请直接出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com