
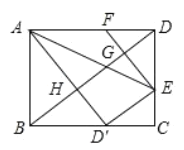
【题目】如图,在矩形ABCD中,E为CD上一点,若△ADE沿直线AE翻折,使点D落在BC边上点![]() 处,F为AD上一点,且
处,F为AD上一点,且![]() ,EF与BD相交于点G,
,EF与BD相交于点G,![]() 与BD相交于点H,
与BD相交于点H,![]() ,HG=2,则BD=__________.
,HG=2,则BD=__________.
【答案】![]()
【解析】
首先证明出△C![]() E∽△BA
E∽△BA![]() ,然后得出
,然后得出![]() ,进一步再证明△EDF∽△DAB,从而结合题意得出EF⊥BD,然后证明出四边形HGE
,进一步再证明△EDF∽△DAB,从而结合题意得出EF⊥BD,然后证明出四边形HGE![]() 是矩形,得出HG=E
是矩形,得出HG=E![]() =DE=2,之后设EC=y,C
=DE=2,之后设EC=y,C![]() =x,通过△BH
=x,通过△BH![]() ∽△
∽△![]() ,表示出BD,然后再通过△DFE∽△CE
,表示出BD,然后再通过△DFE∽△CE![]() 建立方程求出符合题意的y的值,进而计算求出BD即可.
建立方程求出符合题意的y的值,进而计算求出BD即可.
∵四边形ABCD为矩形,
∴∠B=∠C=90°,
∵∠A![]() E=∠D=90°,
E=∠D=90°,
∴∠A![]() +∠E
+∠E![]() =90°,∠E
=90°,∠E![]() =90°,
=90°,
∴∠A![]() ,
,
∴△C![]() ,
,
∴![]() ,
,
∵C![]() =DF,A
=DF,A![]() ,
,![]() ,
,
∴![]() ,
,
∵∠EDF=∠BAD=90°,
∴△EDF∽△DAB,
∴∠FED=∠ADB,
∵∠ADB+∠BDC=90°,
∴∠FED+∠BDC=90°,
∴EF⊥BD,
又∵![]() ∥BD,A
∥BD,A![]() ,
,
∴BD⊥A![]() ,
,
∴四边形HGE![]() 是矩形,
是矩形,
∴HG=E![]() =DE=2,
=DE=2,
设EC=y,C![]() ,
,
易得△EGD≌△![]() ,
,
∴DG=CE=y,EG=C![]() =H
=H![]() ,
,
∵![]() ∥BD,
∥BD,
∴∠E![]() ,
,
∵∠C=∠BH![]() ,
,
∴△BH![]() ∽△
∽△![]()
∴![]() ,
,
∴![]() ,
,
即BH=![]() ,
,
∴BD=BH+GH+DG=![]() ,
,
易得:△DFE∽△CE![]() ,
,
∴![]()
即![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() (舍去),
(舍去),
∴BD=![]() .
.
所以答案为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
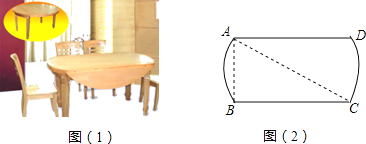
【题目】现在很多家庭都使用折叠型西餐桌来节省空间,两边翻开后成圆形桌面(如图1).餐桌两边AB和CD平行且相等(如图2),小华用皮带尺量出AC=2米,AB=1米,那么桌面翻成圆桌后,桌子面积会增加_____平方米.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,A、B为x轴上两点,C、D为y轴上的两点,经
中,A、B为x轴上两点,C、D为y轴上的两点,经
过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封
闭曲线称为“蛋线”.已知点C的坐标为(0,![]() ),点M是抛物线C2:
),点M是抛物线C2:![]() (
(![]() <0)的顶点.
<0)的顶点.
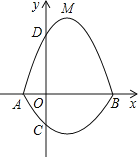
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:![]()
(2)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() ,
,![]() .
.
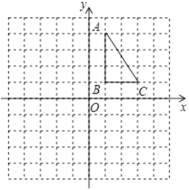
①画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
②画出![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 后的
后的![]() ;
;
③在②的条件下,求线段![]() 扫过的面积(结果保留
扫过的面积(结果保留![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,直线![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于点
轴于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,交
,交![]() 轴于点
轴于点![]() .点
.点![]() 为抛物线上一动点,过点
为抛物线上一动点,过点![]() 作
作![]() 轴的垂线,交直线
轴的垂线,交直线![]() 于点
于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() .
.
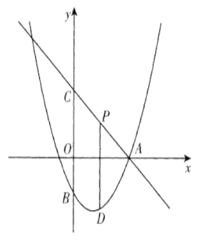
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 下方的抛物线上运动时,求线段
下方的抛物线上运动时,求线段![]() 长度的最大值;
长度的最大值;
(3)若点![]() 是平面内任意一点,是否存在点
是平面内任意一点,是否存在点![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形?若存在,请直接出
为顶点的四边形为菱形?若存在,请直接出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某淘宝网店销售台灯,成本为每个30元.销售大数据分析表明:当每个台灯售价为40元时,平均每月售出600个;若售价每下降1元,其月销售量就增加200个.
(1)若售价下降1元,每月能售出 个台灯,若售价下降x元(![]() ),每月能售出 个台灯.
),每月能售出 个台灯.
(2)为迎接“双十一”,该网店决定降价促销,在库存为1210个台灯的情况下,若预计月获利恰好为8400元,求每个台灯的售价.
(3)月获利能否达到9600元,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com