
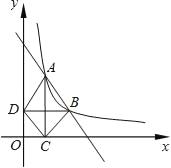
����Ŀ����ͼ����ֱ������ϵƽ���ڣ�����y=![]() ��x��0��m�dz�������ͼ��A��1��4����B��a��b��������a��1������A��x��Ĵ��ߣ�����ΪC������B��y��Ĵ��ߣ�����ΪD������AD��AB��DC��CB��
��x��0��m�dz�������ͼ��A��1��4����B��a��b��������a��1������A��x��Ĵ��ߣ�����ΪC������B��y��Ĵ��ߣ�����ΪD������AD��AB��DC��CB��
��1��������������ʽ��
��2������ABD�����ΪS������a�Ĵ���ʽ��ʾ��S��
��3������ABD�����Ϊ2ʱ���ж��ı���ABCD����״����˵�����ɣ�
���𰸡���1����������������ʽΪy=![]() ����2��S=2a��2����3���ı���ABCDΪ���Σ����ɼ�����.
����2��S=2a��2����3���ı���ABCDΪ���Σ����ɼ�����.
�������������������1����A��1��4������y=![]() ���ô���ϵ������⼴�ɣ�
���ô���ϵ������⼴�ɣ�
��2����B��a��b��������1������ý���ʽ�У����b��a�Ĺ�ϵ�����������ε������ʽ��ʽ���ɣ�
��3����S=2���루2���еĽ���ʽ�У����a��ֵ����֪�ı���ABCD�ĶԽ����ഹֱƽ�֣��Ӷ���֤���ı���ABCDΪ����.
�⣺��1����A��1��4������y=![]() ��m=1��4=4��
��m=1��4=4��
���Է�������������ʽΪy=![]() ��
��
��2����B��a��b������y=![]() ��b=
��b=![]() ��
��
����S=![]() a��4��
a��4��![]() ��=2a��2��
��=2a��2��
��3���ı���ABCDΪ���Σ��������£�
��S=2ʱ��2a��2=2�����a=2��
����AC��BD���ഹֱƽ�֣�
�����ı���ABCDΪ���Σ�


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2��2anx+an2+n+3�Ķ���P��һ����ֱ��l�ϣ�
��1��ֱ��д��ֱ��l�Ľ���ʽ��
��2�������������ʵ��a������ȷ����n��ֵ��ʹ��������x����Ψһ�Ĺ����㣬���ʱn��ֵ��
��3������P��x����ʱ����������ֱ��l����һ������Q������Q��x���ƽ���ߣ����������ڵ�A������Q��y���ƽ���ߣ���x���ڵ�B����![]() ��ֵ��ȡֵ��Χ��
��ֵ��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��DΪBC����һ�㣬��B=30����DAB=45�㣮��1�����DAC�Ķ�������2����˵����AB=CD��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������̼����,��ɫ������������ռ�,����Դ��������Ϊ����ϲ���Ľ�ͨ����.ij�������۹�˾�ƻ�����һ������Դ�������Խ�������,���˽�2��A��������3��B���������Ľ��۹���80��Ԫ��3��A��������2��B�������Ľ��۹���95��Ԫ��
(1)��A��B�����ͺŵ�����ÿ�����۷ֱ�Ϊ���ٷ�Ԫ?
(2)���ù�˾�ƻ�������200��Ԫ�������������ͺŵ�����Դ����(�����ͺŵ�����������)����������ù�˾��ƹ�����
(3)�����������۹�˾����1��A�������ɻ���8000Ԫ,����1��B�������ɻ���5000Ԫ,��(2)�еĹ�����,������Щ����Դ����ȫ���۳�,���ַ����������?��������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
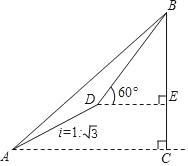
����Ŀ����ͼ��ij����С��Ϊ�˲���ɽBC�ĸ߶ȣ��ڵ���A�����ɽ��B������45����Ȼ�������¶�Ϊi=1��![]() ������AD����200�״ﵽD������ʱ��D�����ɽ��B������Ϊ60������ɽ��BC������������ţ���
������AD����200�״ﵽD������ʱ��D�����ɽ��B������Ϊ60������ɽ��BC������������ţ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
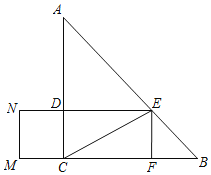
����Ŀ����ͼ��Rt��ABC�У���ACB��90����AC��BC��3cm����DΪAC����һ�㣨�����A��C�غϣ�����CDΪ�ߣ�����������������CDEF��������������������CDMN���Ҷ���E��F�ֱ��ڱ�AB��BC�ϣ�����CE����AD�ij�Ϊxcm������EFMN�����Ϊy1cm2����ACE�����Ϊy2cm2
��1����գ�y1��x�ĺ�����ϵʽ���� ����y2��x�ĺ�����ϵʽ���� �����Ա���x��ȡֵ��Χ���� ����
��2����ƽ��ֱ������ϵ�У�����������������ͼ��
��3����ϻ����ĺ���ͼ������⣺������EFNM�����С����ACE�����ʱ��x��ȡֵ��Χ���� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���н���ԱԤ��һ��Ӧ��ˮ���ܳ����г�����3000Ԫ������һ������ˮ�������к��Ȼ����Ӧ��ȫ�����꣬���н���Ա����1500Ԫ�����˵ڶ�������ˮ���������۱ȵ�һ��������50%��������ˮ����ƽ���۸�Ϊ9Ԫ/kg
��1������һ������ˮ���ĵ��ۣ�
��2����һ��ˮ�������۵���Ϊ10Ԫ/kg���ڶ���ˮ�������۵���Ϊ15Ԫ/kg�����ڵڶ���ˮ�������۹����з����������ã����о����ڶ���ˮ������һ��������ʣ��ˮ����ԭ�ۼ۵�7�����ۣ�Ҫʹ����ˮ��ȫ�����ۺ���������900Ԫ���ʵڶ���ˮ����ԭ���۵����������۶���ǧ�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����8������ͼ��AC��ABCD��һ���Խ��ߣ���AC�е�O��ֱ�߷ֱ�AD��BC�ڵ�E��F��
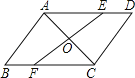
��1����֤����AOE�ա�COF��
��2����EF��AC����ʲô����ʱ���ı���AFCE�����Σ���˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����CΪ�߶�AB��һ�㣬�ֱ���AB��AC��CBΪ��������Ϊ120���ĵ��������Σ����Ƕ���ֱ�ΪD��E��F����E��F��AB��ͬ�࣬��D����һ�ࣩ
��1����ͼ1������C��AB���е㣬���AED���� ����
��2����ͼ2������C����AB���е�
����֤����DEFΪ�ȱ������Σ�
������CD������ADC��90�㣬AB��3����ֱ��д��EF�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com