
【题目】如图,点C为线段AB上一点,分别以AB、AC、CB为底作顶角为120°的等腰三角形,顶角顶点分别为D、E、F(点E、F在AB的同侧,点D在另一侧)
(1)如图1,若点C是AB的中点,则∠AED= ;
(2)如图2,若点C不是AB的中点
①求证:△DEF为等边三角形;
②连接CD,若∠ADC=90°,AB=3,请直接写出EF的长.

【答案】(1) 90°;(2)①见解析;②![]()
【解析】
(1)如图1,过E作EH⊥AB于H,连接CD,设EH=x,则AE=2x,AH=![]() x,根据等腰三角形的性质得到∠DAC=30°,进而得到DC=CE,又因为EH∥DC,∴∠HED=∠EDC=∠CED,再进一步得到∠AEH=60°,∠HED=30°,即可求出∠AED的大小;(2)①延长FC交AD于H,连接HE,如图2,根据等腰三角形的性质得到∠FCB=∠FBC=30°,∠DAB=∠DBA=30°,∠EAC=∠ECA=30°,进而得到AD∥EC∥BF,AE∥CF∥BD,所以四边形BDHF、四边形AECH是平行四边形,进而得到△AEH是等边三角形,再根据SAS判定定理得到△DHE≌△FCE,∴∠DEF=∠CEH=60°,∴△DEF是等边三角形;②如图3,过E作EM⊥AB于M,根据等腰三角形的性质,求出CD、CE的长,再根据勾股定理求出DE的长,因为△DEF是等边三角形,∴EF=DE,即可得解.
x,根据等腰三角形的性质得到∠DAC=30°,进而得到DC=CE,又因为EH∥DC,∴∠HED=∠EDC=∠CED,再进一步得到∠AEH=60°,∠HED=30°,即可求出∠AED的大小;(2)①延长FC交AD于H,连接HE,如图2,根据等腰三角形的性质得到∠FCB=∠FBC=30°,∠DAB=∠DBA=30°,∠EAC=∠ECA=30°,进而得到AD∥EC∥BF,AE∥CF∥BD,所以四边形BDHF、四边形AECH是平行四边形,进而得到△AEH是等边三角形,再根据SAS判定定理得到△DHE≌△FCE,∴∠DEF=∠CEH=60°,∴△DEF是等边三角形;②如图3,过E作EM⊥AB于M,根据等腰三角形的性质,求出CD、CE的长,再根据勾股定理求出DE的长,因为△DEF是等边三角形,∴EF=DE,即可得解.
(1)如图1,过E作EH⊥AB于H,连接CD,
设EH=x,则AE=2x,AH=![]() x,
x,
∵AE=EC,
∴AC=2AH=2![]() x,
x,
∵C是AB的中点,AD=BD,
∴CD⊥AB,
∵∠ADB=120°,
∴∠DAC=30°,
∴DC=2x,
∴DC=CE=2x,
∵EH∥DC,
∴∠HED=∠EDC=∠CED,
∵∠AEH=60°,∠AEC=120°,
∴∠HEC=60°,
∴∠HED=30°,
∴∠AED=∠AEH+∠HED=90°;
故答案为:90°;
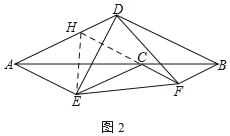
(2)①延长FC交AD于H,连接HE,如图2,
∵CF=FB,
∴∠FCB=∠FBC,
∵∠CFB=120°,
∴∠FCB=∠FBC=30°,
同理:∠DAB=∠DBA=30°,∠EAC=∠ECA=30°,
∴∠DAB=∠ECA=∠FBD,
∴AD∥EC∥BF,
同理AE∥CF∥BD,
∴四边形BDHF、四边形AECH是平行四边形,
∴EC=AH,BF=HD,
∵AE=EC,
∴AE=AH,
∵∠HAE=60°,
∴△AEH是等边三角形,
∴AE=AH=HE=CE,∠AHE=∠AEH=60°,
∴∠DHE=120°,
∴∠DHE=∠FCE.
∵DH=BF=FC,
∴△DHE≌△FCE(SAS),
∴DE=EF,∠DEH=∠FEC,
∴∠DEF=∠CEH=60°,
∴△DEF是等边三角形;
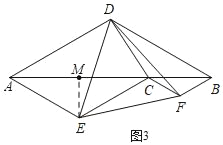
②如图3,过E作EM⊥AB于M,
∵∠ADC=90°,∠DAC=30°,
∴∠ACD=60°,
∵∠DBA=30°,
∴∠CDB=∠DBC=30°,
∴CD=BC=![]() AC,
AC,
∵AB=3,
∵AC=2,BC=CD=1,
∵∠ACE=30°,∠ACD=60°,
∴∠ECD=30°+60°=90°,
∵AE=CE,
∴CM=![]() AC=1,
AC=1,
∵∠ACE=30°,
∴CE=![]() ,
,
Rt△DEC中,DE=![]() =
=![]() =
=![]() ,
,
由①知:△DEF是等边三角形,
∴EF=DE=![]() .
.


科目:初中数学 来源: 题型:
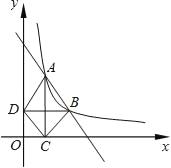
【题目】如图,在直角坐标系平面内,函数y=![]() (x>0,m是常数)的图象经过A(1,4)、B(a,b),其中a>1,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD,AB,DC,CB.
(x>0,m是常数)的图象经过A(1,4)、B(a,b),其中a>1,过点A作x轴的垂线,垂足为C,过点B作y轴的垂线,垂足为D,连接AD,AB,DC,CB.
(1)求反比例函数解析式;
(2)当△ABD的面积为S,试用a的代数式表示求S.
(3)当△ABD的面积为2时,判断四边形ABCD的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC的一边AB上有一点P.
(1)能否在另外两边AC和BC上各找一点M、N,使得△PMN的周长最短.若能,请画出点M、N的位置,若不能,请说明理由;
(2)若∠ACB=40°,在(1)的条件下,求出∠MPN的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道对于一个图形,通过不同的方法计算图形的面积时,可以得到一个数学等式.例如由图1可以得到![]() .请回答下列问题:
.请回答下列问题:

(1)写出图2中所表示的数学等式是 ;
(2)如图3,用四块完全相同的长方形拼成正方形,用不同的方法,计算图中阴影部分的面积,你能发现什么?(用含有![]() ,
,![]() 的式子表示) ;
的式子表示) ;
(3)通过上述的等量关系,我们可知: 当两个正数的和一定时,它们的差的绝对值越小,则积越 (填“ 大”“或“小”);当两个正数的积一定时,它们的差的绝对值越小,则和越 (填“ 大”或“小”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料:
∵![]() =
=![]() ×
×![]() ,
,![]() =
=![]() ×
×![]() ,
,![]() =
=![]() ×
×![]() ,…,
,…,![]() =
=![]() ×
×![]() ,
,
∴![]() +
+![]() +
+![]() +…+
+…+![]() =
=![]() ×
×![]() +
+![]() ×
×![]() +
+![]() ×
×![]() +…+
+…+![]() ×
×![]()
=![]() ×
×![]() =
=![]() ×
×![]() =
=![]() .
.
请解答下列问题:
(1)在和式![]() +
+![]() +
+![]() +…中,第100项是 ;
+…中,第100项是 ;
(2)化简![]() +
+![]() +
+![]() +…+
+…+![]() ,并求n=100时分式的值;
,并求n=100时分式的值;
(3)根据上面的方法,解方程:![]() +
+![]() +
+![]() =
=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
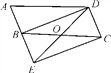
【题目】如图,将□ABCD的边AB延长至点E,使AB=BE,连接BD,DE,EC,DE交BC于点O.
(1)求证:△ABD≌△BEC;
(2)若∠BOD=2∠A,求证:四边形BECD是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,乙从B地到A地需要( )分钟
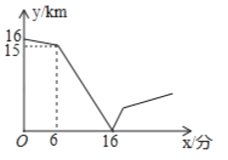
A.12B.14C.18D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着私家车的增加,城市的交通也越老越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车行驶速度低于20千米/时,交通就会拥堵,为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是( )
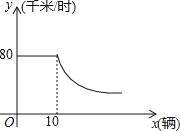
A. x≤40 B. x≥40 C. x>40 D. x<40
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com