
【题目】以下四个命题:①如果三角形一边的中点到其他两边距离相等,那么这个三角形一定是等腰三角形:②两条对角线互相垂直且相等的四边形是正方形:③一组数据2,4,6.4的方差是2;④△OAB与△OCD是以O为位似中心的位似图形,且位似比为1:4,已知∠OCD=90°,OC=CD.点A、C在第一象限.若点D坐标为(2 ![]() ,0),则点A坐标为(
,0),则点A坐标为( ![]() ,
, ![]() ),其中正确命题有(填正确命题的序号即可)
),其中正确命题有(填正确命题的序号即可)
【答案】①③④
【解析】解:①如果三角形一边的中点到其他两边距离相等,那么这个三角形一定是等腰三角形,故①正确; ②两条对角线互相垂直且相等的四边形是正方形或等腰梯形,故②错误;
③一组数据2,4,6.4的方差是2,故③正确;
④△OAB与△OCD是以O为位似中心的位似图形,且位似比为1:4,已知∠OCD=90°,OC=CD.
点A、C在第一象限.若点D坐标为(2 ![]() ,0)得,C(
,0)得,C( ![]() ,
, ![]() ).
).
由位似比为1:4,得
点A坐标为( ![]() ,
, ![]() ),故④正确;
),故④正确;
所以答案是:①③④.
【考点精析】根据题目的已知条件,利用命题与定理的相关知识可以得到问题的答案,需要掌握我们把题设、结论正好相反的两个命题叫做互逆命题.如果把其中一个叫做原命题,那么另一个叫做它的逆命题;经过证明被确认正确的命题叫做定理.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
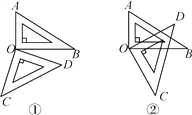
【题目】如图①所示,将一副三角尺的直角顶点重合在点O处.
(1)①∠AOD和∠BOC相等吗?(不要求说明理由)
②∠AOC和∠BOD在数量上有何种关系?(不要求说明理由)
(2)若将这副三角尺按如图②摆放,三角尺的直角顶点重合在点O处.
①∠AOD和∠BOC相等吗?说明理由;
②∠AOC和∠BOD在数量上有何种关系?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
空调 | 彩电 | |
进价(元/台) | 5400 | 3500 |
售价(元/台) | 6100 | 3900 |
设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择?
(3)选择哪种进货方案,商场获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价![]() 元,领带每条定价
元,领带每条定价![]() 元.厂方在开展促销活动期间,可以同时向客户提供两种优惠方案:
元.厂方在开展促销活动期间,可以同时向客户提供两种优惠方案:
![]() 买一套西装送一条领带;
买一套西装送一条领带;
![]() 西装和领带都按定价的
西装和领带都按定价的![]() 付款.现某客户要到该服装厂购买西装
付款.现某客户要到该服装厂购买西装![]() 套,领带
套,领带![]() 条
条![]() 超过
超过![]() .
.
![]() 若该客户按方案
若该客户按方案![]() 购买,需付款________元(用含
购买,需付款________元(用含![]() 的式子表示);若该客户按方案
的式子表示);若该客户按方案![]() 购买,需付款________元(用含
购买,需付款________元(用含![]() 的式子表示);
的式子表示);
![]() 若
若![]() ,通过计算说明此时按哪种方案购买较为合算?
,通过计算说明此时按哪种方案购买较为合算?
![]() 当
当![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P,Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,开口向下的抛物线y=ax2+bx+c交y轴于A点,交x轴于B、C两点(点B在点C的左侧).已知A点坐标为(0,﹣5),BC=4,抛物线过点(2,3).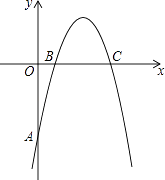
(1)求此抛物线的解析式;
(2)记抛物线的顶点为M,求△ACM的面积;
(3)在抛物线上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某年6月份的日历.
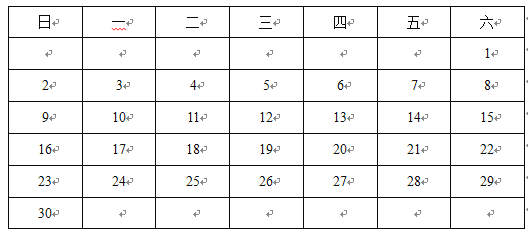
(1)细心观察:小张一家外出旅游5天,这5天的日期之和是20.小张旅游最后一天是 _____________号.
(2)如果用一个长方形方框任意框出3![]() 3个数,从左下角到右上角的“对角线”上的3个数字的和54,那么这9个数的和为______________,在这9个日期中,最后一天是_____________号.
3个数,从左下角到右上角的“对角线”上的3个数字的和54,那么这9个数的和为______________,在这9个日期中,最后一天是_____________号.
![]()
(3)在这个月的日历中,用方框能否圈出“总和为135”的9个数?如果能,请求出这9个日期分别是几号;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,我们把对角线互相垂直的四边形叫做垂美四边形.

(l)概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由.
(2)性质探宄:试探索垂美四边形ABCD两组对边AB,CD与BC,AD之间的数量关系.
猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证)
(3)问题解决:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连接CE,BG,GE,已知AC=4,AB=5,求GE长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com