
【题目】如图,在平面直角坐标系中,开口向下的抛物线y=ax2+bx+c交y轴于A点,交x轴于B、C两点(点B在点C的左侧).已知A点坐标为(0,﹣5),BC=4,抛物线过点(2,3).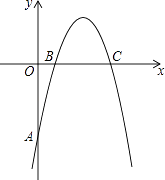
(1)求此抛物线的解析式;
(2)记抛物线的顶点为M,求△ACM的面积;
(3)在抛物线上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:由点A的坐标为(0,﹣5)可知c=﹣5,
又∵抛物线经过点(2,3),
∴4a+2b﹣5=0①,
设B(x1,0),C(x2,0),则(x1﹣x2)2=16.即(x1+x2)2﹣2x1x2=16.
∵x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
∴ ![]() +
+ ![]() =16②.
=16②.
将方程①与方程②联立,解得:a=﹣1,b=6.
∴抛物线的解析式为y=﹣x2+6x﹣5
(2)
解:如图1所示:记AM与x轴的交点坐标为D.

∵y=﹣x2+6x﹣5=﹣(x﹣3)2+4,
∴点M的坐标为(3,4).
设直线AM的解析式为y=kx+b.
∵将A(0,﹣5)、M(3,4)代入得 ![]() ,解得:k=3,b=﹣5,
,解得:k=3,b=﹣5,
∴直线AM的解析式为y=3x﹣5.
∵令y=0得:3x﹣5=0.解得:x= ![]() ,
,
∴D( ![]() ,0).
,0).
∵令抛物线的y=0得:﹣x2+6x﹣5=0,解得x1=1,x2=5,
∴C(5,0).
∴S△ACM=S△CDA+S△CDM= ![]() ×(5﹣
×(5﹣ ![]() )×(4+5)=15
)×(4+5)=15
(3)
解:①当∠PCA=90°时,如图2所示:过点C作CP⊥AC,交抛物线与点P.
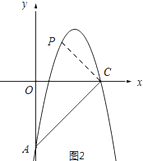
设AC的解析式为y=kx+b.
∵将点A、C的坐标代入得: ![]() ,解得:k=1,b=﹣5,
,解得:k=1,b=﹣5,
∴直线AC的解析式为y=x﹣5.
设PC的解析式为y=k1x+b1.
∵PC⊥AC,
∴k1=﹣1.
∴直线PC的解析式为y=﹣x+b1.
∵将C(5,0)代入得:﹣5+b=0,解得;b=5,
∴PC的解析式为y=﹣x+5.
∵将y=﹣x+5代入y=﹣x2+6x﹣5得:﹣x2+6x﹣5=﹣x+5,整理得:x2﹣7x+10=0,解得;x1=2,x2=5(舍去).
∴点P的坐标为(2,3)
②当∠PAC=90°时,如图3所示:
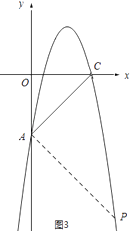
∵AP⊥AC,A(0,﹣5)
∴AP的解析式为y=﹣x﹣5.
将y=﹣x﹣5代入y=﹣x2+6x﹣5得:﹣x2+6x﹣5=﹣x﹣5,整理得:x2﹣7x=0,解得;x1=7,x2=0(舍去).
∴点P的坐标为(7,﹣12).
综上所述点P的坐标为(2,3)或(7,12)
【解析】(1)由点A的坐标可求得c的值,将(2,3)代入抛物线的解析式得到关于a、b的二元一次方程,设B(x1 , 0),C(x2 , 0),由题意可得到(x1﹣x2)2=16.结合一元二次方程根与系数的关系可得到关于a、b的另一个方程,将两个方程联立可求得a、b的值,从而得到抛物线的解析式;(2)记AM与x轴的交点坐标为D.先求得点M的坐标,从而可求得AM的解析式,然后再求得点D的坐标,最后依据S△ACM=S△CDA+S△CDM求解即可;(3)先求得AC的解析式,①当∠PCA=90°时,可求得PC的解析式,然后求得PC与抛物线的交点坐标即可;②当∠PAC=90°时,可求得PC的解析式然后求得PC与抛物线的交点坐标即可.
【考点精析】认真审题,首先需要了解二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点),还要掌握二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.

(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的对角线AC上的一个动点(不与A、C重合),作EF⊥AC交边BC于点F,联结AF、BE交于点G. 
(1)求证:△CAF∽△CBE;
(2)若AE:EC=2:1,求tan∠BEF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四个命题:①如果三角形一边的中点到其他两边距离相等,那么这个三角形一定是等腰三角形:②两条对角线互相垂直且相等的四边形是正方形:③一组数据2,4,6.4的方差是2;④△OAB与△OCD是以O为位似中心的位似图形,且位似比为1:4,已知∠OCD=90°,OC=CD.点A、C在第一象限.若点D坐标为(2 ![]() ,0),则点A坐标为(
,0),则点A坐标为( ![]() ,
, ![]() ),其中正确命题有(填正确命题的序号即可)
),其中正确命题有(填正确命题的序号即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一架方梯AB长25米,如图所示,斜靠在一面上:

(1)若梯子底端离墙7米,这个梯子的顶端距地面有多高?
(2)在(1)的条件下,如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,CD=3cm,则AF的长为( ) 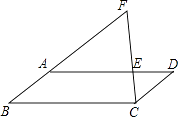
A.5cm
B.6cm
C.7cm
D.8cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组开展了一次课外活动,过程如下:
如图①,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合,三角板的一边交AB于点P,另一边交BC的延长线于点Q.

(1)求证:AP=CQ;
(2)如图②,小明在图①的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并证明.
(3)如图③,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC的延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△ DEQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华和小容都想参加学校组织的数学兴趣小组,根据学校分配的名额,他们两人只能有1人参加.数学老师想出了一个主意:如图,给他们六张卡片,每张卡片上都有一些数,将化简后的数在数轴上表示出来,再用“<”连接起来,谁先按照要求做对,谁就参加兴趣小组,你也一起来试一试吧!
-(-2) (-1)3 -|-3| 0的相反数
① ② ③ ④
-0.4的倒数 比-1大2.5的数
⑤ ⑥
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com