
����Ŀ����ѧ��ȤС�鿪չ��һ�ο������������£�
��ͼ�٣�������ABCD�У�AB=6�������ǰ����������ABCD�ϣ�ʹ���ǰ��ֱ�Ƕ�����D���غϣ����ǰ��һ�߽�AB�ڵ�P����һ�߽�BC���ӳ����ڵ�Q��

��1����֤��AP=CQ��
��2����ͼ�ڣ�С����ͼ�ٵĻ���������PDQ��ƽ����DE��BC�ڵ�E������PE��������PE��QE����һ����������ϵ����²����Ľ��۲�֤����
��3����ͼ�ۣ��̶����ǰ�ֱ�Ƕ�����D�㲻����ת�����ǰ壬ʹ���ǰ��һ�߽�AB���ӳ����ڵ�P����һ�߽�BC���ӳ����ڵ�Q��������PDQ��ƽ����DE��BC���ӳ����ڵ�E������PE����AB��AP=3��4�����С������� DEQ�������
���𰸡���1��֤������������2��PE=QE��֤������������3��![]()
��������������(1)��ASA֤����ADP�ա�CDQ��(2)��SAS֤����DEP�ա�DEQ��(3)��QE��PE��x����BE��14��x����Rt��BPE�У��ɹ��ɶ�����QE����S��DEQ���֡�DEP�ա�DEQ��������.
��⣺(1)֤�����ߡ�ADC����PDQ��90�������ADP����CDQ��
����ADP����CDQ����DAP����DCQ��90����AD��CD����ADP����CDQ��
���ADP�ա�CDQ(ASA)����AP��CQ��
(2)PE��QE��
֤������(1)��֪��ADP�ա�CDQ����DP��DQ��
��DEƽ�֡�PDQ�����PDE����QDE.
����DEP����DEQ��DP��DQ����PDE����QDE��DE��DE.
���DEP�ա�DEQ(SAS)��PE��QE��
(3)�⣺��AB��AP��3��4��AB��6����AP��8��BP��2��
��(1)ͬ��������֤����ADP�ա�CDQ����CQ��AP��8��
��(2)ͬ��������֤����DEP�ա�DEQ����PE��QE��
��QE��PE��x����BE��BC��CQ��QE��14��x��
��Rt��BPE�У��ɹ��ɶ����ã�
��ã�x��![]() ����QE��
����QE��![]() ��
��
��S��DEQ��![]() QECD��
QECD��![]() ��
��![]() ��6��
��6��![]() ��
��
�ߡ�DEP�ա�DEQ��
��S��DEP��S��DEQ��![]() ��
��


 Сѧ��10���ӿ������100��ϵ�д�
Сѧ��10���ӿ������100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
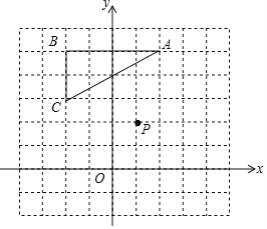
����Ŀ������ͼ��ʾ������ֽ�У�������ƽ��ֱ������ϵxOy����P��1��2������A��2��5����B��-2��5����C��-2��3����
��1���Ե�PΪ�Գ����ģ�������A��B��C����ʹ��A��B��C�����ABC���ڵ�P�Գƣ���д�����е�����꣺B��________��C��________��
��2�������ABCA��B��C���������__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��װ������һ����װ���������װÿ����![]() Ԫ�����ÿ������
Ԫ�����ÿ������![]() Ԫ�������ڿ�չ������ڼ䣬����ͬʱ��ͻ��ṩ�����Żݷ�����
Ԫ�������ڿ�չ������ڼ䣬����ͬʱ��ͻ��ṩ�����Żݷ�����
![]() ��һ����װ��һ�������
��һ����װ��һ�������
![]() ��װ������������۵�
��װ������������۵�![]() �����ij�ͻ�Ҫ���÷�װ��������װ
�����ij�ͻ�Ҫ���÷�װ��������װ![]() �ף����
�ף����![]() ��
��![]() ����
����![]() ��
��
![]() ���ÿͻ�������
���ÿͻ�������![]() �����踶��________Ԫ���ú�
�����踶��________Ԫ���ú�![]() ��ʽ�ӱ�ʾ�������ÿͻ�������
��ʽ�ӱ�ʾ�������ÿͻ�������![]() �����踶��________Ԫ���ú�
�����踶��________Ԫ���ú�![]() ��ʽ�ӱ�ʾ����
��ʽ�ӱ�ʾ����
![]() ��
��![]() ��ͨ������˵����ʱ�����ַ��������Ϊ���㣿
��ͨ������˵����ʱ�����ַ��������Ϊ���㣿
![]() ��
��![]() ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����������������Ǯ����
ʱ�����ܸ���һ�ָ�ΪʡǮ�Ĺ�������д����Ĺ�����������������Ǯ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��������µ�������y=ax2+bx+c��y����A�㣬��x����B��C���㣨��B�ڵ�C����ࣩ����֪A������Ϊ��0����5����BC=4�������߹��㣨2��3����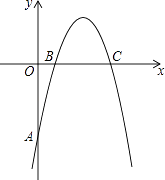
��1����������ߵĽ���ʽ��
��2���������ߵĶ���ΪM�����ACM�������
��3�������������Ƿ���ڵ�P��ʹ��ACP����ACΪֱ�DZߵ�ֱ�������Σ������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ���ɳ�
���ɳ�![]() ��ͬѧ�μ���ѧ��������ʦ��
��ͬѧ�μ���ѧ��������ʦ��![]() ��Ϊ�����ѷ�������
��Ϊ�����ѷ�������![]() �ֵIJ��ּ�Ϊ���������㲿�ּ�Ϊ���������ּ�¼���£�
�ֵIJ��ּ�Ϊ���������㲿�ּ�Ϊ���������ּ�¼���£�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
![]() ��
��![]() ��ͬѧ����߷ֺ���ͷָ��Ƕ��٣�
��ͬѧ����߷ֺ���ͷָ��Ƕ��٣�
![]() �������ֵĺ͵��ڻ��ֵĸ��ж����ˣ�
�������ֵĺ͵��ڻ��ֵĸ��ж����ˣ�
![]() ��ʮ����ͬѧ��ƽ���ɼ��Ƕ��٣�
��ʮ����ͬѧ��ƽ���ɼ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��6�·ݵ�����.
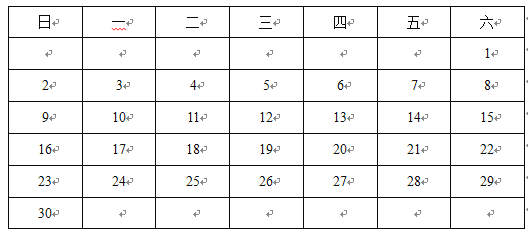
��1��ϸ�Ĺ۲죺С��һ���������5�죬��5�������֮����20.С���������һ���� _____________��.
��2�������һ�������η���������3![]() 3�����������½ǵ����Ͻǵ����Խ������ϵ�3�����ֵĺ�54����ô��9�����ĺ�Ϊ______________������9�������У����һ����_____________��.
3�����������½ǵ����Ͻǵ����Խ������ϵ�3�����ֵĺ�54����ô��9�����ĺ�Ϊ______________������9�������У����һ����_____________��.
![]()
��3��������µ������У��÷����ܷ�Ȧ�����ܺ�Ϊ135����9����������ܣ��������9�����ڷֱ��Ǽ��ţ�������ܣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֽ������һ���ᣨ��ͼ�����۵�ֽ��.
��1����1��ʾ�ĵ��룭1��ʾ�ĵ��غϣ���2��ʾ�ĵ����� ��ʾ�ĵ��غϣ�
��2������1��ʾ�ĵ���5��ʾ�ĵ��غϣ��ش��������⣺
�� 7��ʾ�ĵ����� ��ʾ�ĵ��غϣ�
�� ��������A��B����֮��ľ���Ϊ11��A��B����ࣩ����A��B���㾭�۵���
�غϣ� ��A��B�����ʾ�������Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
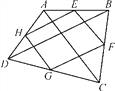
����Ŀ����ͼ��ʾ��E��F��G��H�ֱ����ı���ABCD�ı�AB��BC��CD��AD���е���
(1)���ı���ABCD�Ǿ���ʱ���ı���EFGH��_________����˵�����ɣ�
(2)���ı���ABCD����ʲô����ʱ���ı���EFGHΪ�����Σ���˵��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������:
��1��(��78) +(+5)+(+78) ��2��(+23)+(��17)+(+6)+(��22)
��3��[45��(![]() ��
��![]() +
+![]() )��36]��5 ��4��99
)��36]��5 ��4��99![]() ��(��36)
��(��36)
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com