
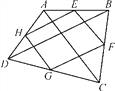
【题目】如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD的中点.
(1)当四边形ABCD是矩形时,四边形EFGH是_________,请说明理由;
(2)当四边形ABCD满足什么条件时,四边形EFGH为正方形?并说明理由.
【答案】(1)菱形,理由见解析;(2)当四边形ABCD满足AC=BD且AC⊥BD时,四边形EFGH为正方形.理由见解析.
【解析】(1)利用三角形中位线定理“三角形的中位线等于第三边的一半”,根据菱形的判定,矩形的性质,求解即可,
(2)首先利用菱形的性质得出平行四边形ABCD是菱形,再利用正方形的性质与判定得出即可.
解:(1)理由:∵四边形ABCD是矩形,∴AC=BD.
由题意,得EF=![]() AC,EH=
AC,EH=![]() BD,GH=
BD,GH=![]() AC,GF=
AC,GF=![]() BD,
BD,
∴EF=EH=GH=GF.
∴四边形EFGH是菱形.
(2)当四边形ABCD满足AC=BD且AC⊥BD时,四边形EFGH为正方形.理由:
∵E,F分别是四边形ABCD的边AB,BC的中点,
∴EF∥AC,EF=![]() AC.
AC.
同理:EH∥BD,EH=![]() BD,GF=
BD,GF=![]() BD,GH=
BD,GH=![]() AC.
AC.
又∵AC=BD,∴EF=EH=GH=GF.
∴四边形EFGH是菱形.
∵AC⊥BD,∴EF⊥EH.
∴四边形EFGH是正方形.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,点E是正方形ABCD的对角线AC上的一个动点(不与A、C重合),作EF⊥AC交边BC于点F,联结AF、BE交于点G. 
(1)求证:△CAF∽△CBE;
(2)若AE:EC=2:1,求tan∠BEF的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学兴趣小组开展了一次课外活动,过程如下:
如图①,正方形ABCD中,AB=6,将三角板放在正方形ABCD上,使三角板的直角顶点与D点重合,三角板的一边交AB于点P,另一边交BC的延长线于点Q.

(1)求证:AP=CQ;
(2)如图②,小明在图①的基础上作∠PDQ的平分线DE交BC于点E,连接PE,他发现PE和QE存在一定的数量关系,请猜测他的结论并证明.
(3)如图③,固定三角板直角顶点在D点不动,转动三角板,使三角板的一边交AB的延长线于点P,另一边交BC的延长线于点Q,仍作∠PDQ的平分线DE交BC的延长线于点E,连接PE,若AB:AP=3:4,请帮小明算出△ DEQ的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华和小容都想参加学校组织的数学兴趣小组,根据学校分配的名额,他们两人只能有1人参加.数学老师想出了一个主意:如图,给他们六张卡片,每张卡片上都有一些数,将化简后的数在数轴上表示出来,再用“<”连接起来,谁先按照要求做对,谁就参加兴趣小组,你也一起来试一试吧!
-(-2) (-1)3 -|-3| 0的相反数
① ② ③ ④
-0.4的倒数 比-1大2.5的数
⑤ ⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
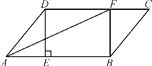
【题目】如图,在□ABCD中,过点D作DE⊥AB于点E,点F在边CD上,CF=AE,连接AF,BF.
(1)求证:四边形BFDE是矩形
(2)若CF=6,BF=8,DF=10,求证:AF是∠DAB的平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十·一”黄金周期间,我市某景点旅游区在7天假期中每天旅游的人数变化如下表:
(正数表示比前一天多的人数,负数表示比前一天少的人数).(单位:万人)
日 期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 | + 1.2 | + 1.2 | + 0.4 | – 0.2 | – 0.8 | + 0.2 | – 1.4 |
若9月30日的旅游人数记为3万人,则
(1)请求出10月5日的旅游人数;
(2)请判断7天内旅游人数最多的是哪一天?最少的是哪一天?它们相差多少万人?
(3)若该景点门票为每人20元,请算出该景点黄金周期间的收入共多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是( )

A. 菱形 B. 矩形 C. 平行四边形 D. 正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com