
【题目】如图,点E是正方形ABCD的对角线AC上的一个动点(不与A、C重合),作EF⊥AC交边BC于点F,联结AF、BE交于点G. 
(1)求证:△CAF∽△CBE;
(2)若AE:EC=2:1,求tan∠BEF的值.
【答案】
(1)证明:∵四边形ABCD是正方形,
∴∠ABC=90°,
∵EF⊥AC,
∴∠FEC=90°=∠ABC,
又∵∠FCE=∠ACB,
∴△CEF∽△CAB,
∴ ![]() ,
,
又∵∠ACF=∠BCE,
∴△CAF∽△CBE
(2)∵△CAF∽△CBE,
∴∠CAF=∠CBE,
∵∠BAC=∠BCA=45°,
∴∠BAF=∠BEF,
设EC=1,则EF=1,FC= ![]() ,
,
∵AE:EC=2:1,
∴AC=3,
∴AB=BC= ![]() AC=
AC= ![]() ,
,
∴BF=BC﹣FC= ![]() ,
,
∴ ![]()
【解析】(1)利用AA证明△CEF∽△CAB,再列出比例式利用SAS证明△CAF∽△CBE(2)证出∴∠BAF=∠BEF,设EC=1,则EF=1,FC= ![]() ,AC=3,由勾股定理得出AB=BC=
,AC=3,由勾股定理得出AB=BC= ![]() AC=
AC= ![]() ,得出BF=BC﹣FC=
,得出BF=BC﹣FC= ![]() ,由三角函数即可得出结果.
,由三角函数即可得出结果.
【考点精析】通过灵活运用正方形的性质和相似三角形的判定与性质,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一次数学活动课上,老师留下了这样一道题“任画一个△ABC,以BC的中点O为对称中心,作△ABC的中心对称图形,问△ABC与它的中心对称图形拼成了一个什么形状的特殊四边形?并说明理由.”
于是大家讨论开了,小亮说:“拼成的是平行四边形”; 小华说:“拼成的是矩形”;
小强说:“拼成的是菱形”; 小红说:“拼成的是正方形”;其他同学也说出了自己的看法……你赞同他们中的谁的观点?为什么?若都不赞同,请说出你的观点(画出图形),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
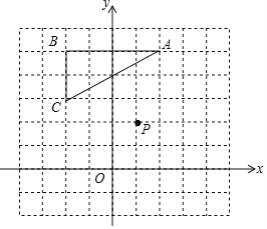
【题目】在如图所示的网格纸中,建立了平面直角坐标系xOy,点P(1,2),点A(2,5),B(-2,5),C(-2,3).
(1)以点P为对称中心,画出△A′B′C′,使△A′B′C′与△ABC关于点P对称,并写出下列点的坐标:B′________,C′________;
(2)多边形ABCA′B′C′的面积是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
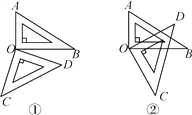
【题目】如图①所示,将一副三角尺的直角顶点重合在点O处.
(1)①∠AOD和∠BOC相等吗?(不要求说明理由)
②∠AOC和∠BOD在数量上有何种关系?(不要求说明理由)
(2)若将这副三角尺按如图②摆放,三角尺的直角顶点重合在点O处.
①∠AOD和∠BOC相等吗?说明理由;
②∠AOC和∠BOD在数量上有何种关系?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
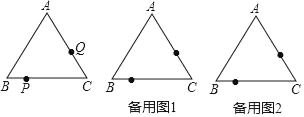
【题目】如图,△ABC是边长为6cm的等边三角形.若点P以1cm/s的速度从点B出发,同时点Q以1.5cm/s的速度从点C出发,都按逆时针方向沿△ABC的边运动,运动时间为6秒.
(1)试求出运动到多少秒时,直线PQ与△ABC的某边平行;
(2)当运动到t1秒时,P、Q对应的点为P1、Q1,当运动到t2秒时(t1≠t2),P、Q对应的点为P2、Q2,试问:△P1CQ1与△P2CQ2能否全等?若能,求出t1、t2的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场筹集资金12.8万元,一次性购进空调、彩电共30台.根据市场需要,这些空调、彩电可以全部销售,全部销售后利润不少于1.5万元,其中空调、彩电的进价和售价见表格.
空调 | 彩电 | |
进价(元/台) | 5400 | 3500 |
售价(元/台) | 6100 | 3900 |
设商场计划购进空调x台,空调和彩电全部销售后商场获得的利润为y元.
(1)试写出y与x的函数关系式;
(2)商场有哪几种进货方案可供选择?
(3)选择哪种进货方案,商场获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装厂生产一种西装和领带,西装每套定价![]() 元,领带每条定价
元,领带每条定价![]() 元.厂方在开展促销活动期间,可以同时向客户提供两种优惠方案:
元.厂方在开展促销活动期间,可以同时向客户提供两种优惠方案:
![]() 买一套西装送一条领带;
买一套西装送一条领带;
![]() 西装和领带都按定价的
西装和领带都按定价的![]() 付款.现某客户要到该服装厂购买西装
付款.现某客户要到该服装厂购买西装![]() 套,领带
套,领带![]() 条
条![]() 超过
超过![]() .
.
![]() 若该客户按方案
若该客户按方案![]() 购买,需付款________元(用含
购买,需付款________元(用含![]() 的式子表示);若该客户按方案
的式子表示);若该客户按方案![]() 购买,需付款________元(用含
购买,需付款________元(用含![]() 的式子表示);
的式子表示);
![]() 若
若![]() ,通过计算说明此时按哪种方案购买较为合算?
,通过计算说明此时按哪种方案购买较为合算?
![]() 当
当![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算出所需的钱数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,开口向下的抛物线y=ax2+bx+c交y轴于A点,交x轴于B、C两点(点B在点C的左侧).已知A点坐标为(0,﹣5),BC=4,抛物线过点(2,3).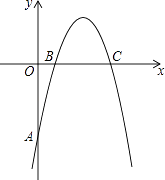
(1)求此抛物线的解析式;
(2)记抛物线的顶点为M,求△ACM的面积;
(3)在抛物线上是否存在点P,使△ACP是以AC为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
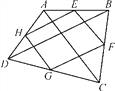
【题目】如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD的中点.
(1)当四边形ABCD是矩形时,四边形EFGH是_________,请说明理由;
(2)当四边形ABCD满足什么条件时,四边形EFGH为正方形?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com