
【题目】已知:如图,在ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是( )

A. 菱形 B. 矩形 C. 平行四边形 D. 正方形
【答案】B
【解析】分析:首先根据平行四边形的判定得出四边形BEDF和四边形AFCE是平行四边形,然后得出四边形MFNE是平行四边形,根据角平分线的性质得出∠BEC=90°,从而说明四边形MFNE是矩形.
详解:∵四边形ABCD是平行四边形, ∴AD=BC,AD∥BC, 又∵DF∥BE,
∴四边形BEDF是平行四边形, ∴DE=BF,ME∥NF,∴AD-DE=BC-BF,即AE=CF,
又∵AE∥CF, ∴四边形AFCE是平行四边形, ∴MF∥NE,
∴四边形MFNE是平行四边形, ∵BE、CE是角平分线,
∴∠EBC+∠ECB=180°×![]() =90°,∴∠BEC=90°,∴四边形MFNE是矩形,故选B.
=90°,∴∠BEC=90°,∴四边形MFNE是矩形,故选B.


科目:初中数学 来源: 题型:
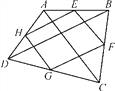
【题目】如图所示,E,F,G,H分别是四边形ABCD的边AB,BC,CD,AD的中点.
(1)当四边形ABCD是矩形时,四边形EFGH是_________,请说明理由;
(2)当四边形ABCD满足什么条件时,四边形EFGH为正方形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:
(1)(-78) +(+5)+(+78) (2)(+23)+(-17)+(+6)+(-22)
(3)[45-(![]() -
-![]() +
+![]() )×36]÷5 (4)99
)×36]÷5 (4)99![]() ×(-36)
×(-36)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆分别与AB、AC边相切于D、E两点,连接OD.已知BD=2,AD=3.求: 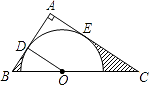
(1)tanC;
(2)图中两部分阴影面积的和.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a﹣2b,2﹣4ab)在抛物线y=x2+4x+10上,则点A关于抛物线对称轴的对称点坐标为( )
A.(﹣3,7)
B.(﹣1,7)
C.(﹣4,10)
D.(0,10)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,下面说法正确的个数是( )个.
①若O是△ABC的外心,∠A=50°,则∠BOC=100°;
②若O是△ABC的内心,∠A=50°,则∠BOC=115°;
③若BC=6,AB+AC=10,则△ABC的面积的最大值是12;
④△ABC的面积是12,周长是16,则其内切圆的半径是1.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有2个信封A、B,信封A装有四张卡片上分别写有1、2、3、4,信封B装有三张卡片分别写有5、6、7,每张卡片除了数字没有任何区别.从这两个信封中随机抽取两张卡片.
(1)请你用列表法或画树状图的方法描述所有可能的结果;
(2)把卡片上的两个数相加,求“得到的和是3的倍数”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某科技开发公司研制出一种新型的产品,每件产品的成本为2400元,销售单价定为3000元,在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600元?
(2)设商家一次购买这种产品x件,开发公司所获得的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获得的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获得的利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A坐标为(2,4),直线x=2与x轴相交于点B,抛物线y=x2的顶点在直线AO上运动,与直线x=2交于点P,设平移后的抛物线顶点M的横坐标为m.
(1)如图1,若m=﹣1,求点P的坐标;
(2)在抛物线平移的过程中,当△PMA是等腰三角形时,求m的值;
(3)如图2,当线段BP最短时,相应的抛物线上是否存在点Q,使△QMA的面积与△PMA的面积相等?若存在,请求出点Q的坐标;若不存在,请说明理由.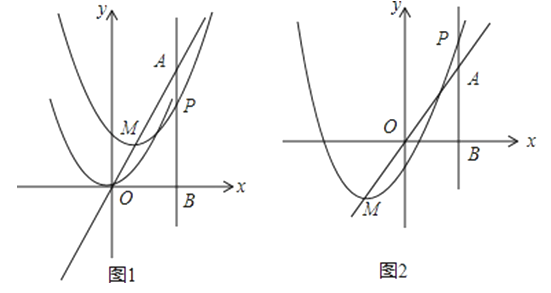
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com