
【题目】某科技开发公司研制出一种新型的产品,每件产品的成本为2400元,销售单价定为3000元,在该产品的试销期间,为了促销,鼓励商家购买该新型产品,公司决定商家一次购买这种新型产品不超过10件时,每件按3000元销售;若一次购买该种产品超过10件时,每多购买一件,所购买的全部产品的销售单价均降低10元,但销售单价均不低于2600元.
(1)商家一次购买这种产品多少件时,销售单价恰好为2600元?
(2)设商家一次购买这种产品x件,开发公司所获得的利润为y元,求y(元)与x(件)之间的函数关系式,并写出自变量x的取值范围.
(3)该公司的销售人员发现:当商家一次购买产品的件数超过某一数量时,会出现随着一次购买的数量的增多,公司所获得的利润反而减少这一情况.为使商家一次购买的数量越多,公司所获得的利润越大,公司应将最低销售单价调整为多少元?(其它销售条件不变)
【答案】解:(1)设件数为x,依题意,得3000﹣10(x﹣10)=2600,解得x=50,
答:商家一次购买这种产品50件时,销售单价恰好为2600元;
(2)当0≤x≤10时,y=(3000﹣2400)x=600x,
当10<x≤50时,y=[3000﹣10(x﹣10)﹣2400]x,即y=﹣10x2+700x
当x>50时,y=(2600﹣2400)x=200x
∴
【解析】(1)设件数为x,则销售单价为3000﹣10(x﹣10)元,根据销售单价恰好为2600元,列方程求解;
(2)由利润y=(销售单价﹣成本单价)×件数,及销售单价均不低于2600元,按0≤x≤10,10<x≤50,x>50三种情况列出函数关系式;
(3)由(2)的函数关系式,利用二次函数的性质求利润的最大值,并求出最大值时x的值,确定销售单价.


科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是( )

A. 菱形 B. 矩形 C. 平行四边形 D. 正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,对角线AC,BD相交于点O.
(1)如图1,点P是正方形ABCD外一点,连接OP,以OP为一边,作正方形OPMN,且边ON与边BC相交,连接AP,BN.
①依题意补全图1;
②判断AP与BN的数量关系及位置关系,写出结论并加以证明;
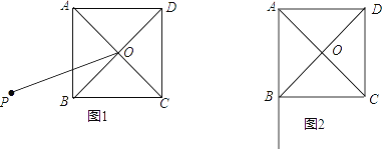
(2)点P在AB延长线上,且∠APO=30°,连接OP,以OP为一边,作正方形OPMN,且边ON与BC的延长线恰交于点N,连接CM,若AB=2,求CM的长(不必写出计算结果,简述求CM长的过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识解答下列问题:
(1) 数轴上表示3的点和2的点两点间的距离为________;
(2)如果在数轴上表示数a的点与表示 - 2的点的距离是3,那么a=________
(3)如果数轴上表示数a的点位于 -4与2之间,则![]() =_________
=_________
(4)a=_____时,![]() 有最小值,且最小值=________________
有最小值,且最小值=________________
(5)直接回答:当式子![]() 取最小值时,相应的a的取值范围是什么?
取最小值时,相应的a的取值范围是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司专销产品![]() ,第一批产品
,第一批产品![]() 上市40天内全部售完.该公司对第一批产品
上市40天内全部售完.该公司对第一批产品![]() 上市后的市场销售情况进行了跟踪调查,调查结果如图所示,其中图1中的折线表示的是市场日销售量与上市时间的关系;图2中的折线表示的是每件产品
上市后的市场销售情况进行了跟踪调查,调查结果如图所示,其中图1中的折线表示的是市场日销售量与上市时间的关系;图2中的折线表示的是每件产品![]() 的销售利润与上市时间的关系.
的销售利润与上市时间的关系.
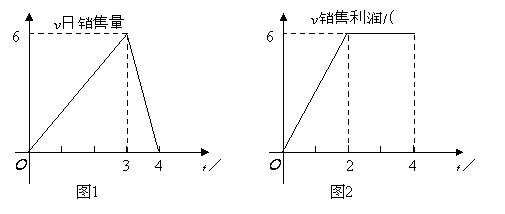
(1)试写出第一批产品![]() 的市场日销售量
的市场日销售量![]() 与上市时间的关系式;
与上市时间的关系式;
(2)第一批产品![]() 上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?(说明理由)
上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?(说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
(1)用含 ![]() 的代数式表示地面的总面积
的代数式表示地面的总面积 ![]() ;
;

(2)已知 ![]() ,且客厅面积是卫生间面积的
,且客厅面积是卫生间面积的 ![]() 倍,如果铺
倍,如果铺 ![]() 平方米地砖的平均费用为
平方米地砖的平均费用为 ![]() 元,那么小王铺地砖的总费用为多少元?
元,那么小王铺地砖的总费用为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com