
����Ŀ��ij��˾ר����Ʒ![]() ����һ����Ʒ
����һ����Ʒ![]() ����40����ȫ�����꣮�ù�˾�Ե�һ����Ʒ
����40����ȫ�����꣮�ù�˾�Ե�һ����Ʒ![]() ���к���г�������������˸��ٵ��飬��������ͼ��ʾ������ͼ1�е����߱�ʾ�����г���������������ʱ��Ĺ�ϵ��ͼ2�е����߱�ʾ����ÿ����Ʒ
���к���г�������������˸��ٵ��飬��������ͼ��ʾ������ͼ1�е����߱�ʾ�����г���������������ʱ��Ĺ�ϵ��ͼ2�е����߱�ʾ����ÿ����Ʒ![]() ����������������ʱ��Ĺ�ϵ��
����������������ʱ��Ĺ�ϵ��
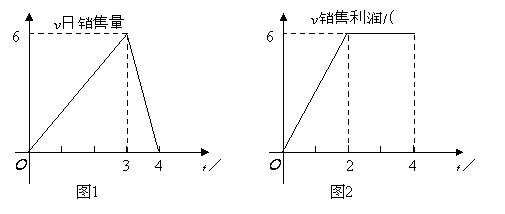
��1����д����һ����Ʒ![]() ���г���������
���г���������![]() ������ʱ��Ĺ�ϵʽ��
������ʱ��Ĺ�ϵʽ��
��2����һ����Ʒ![]() ���к���һ����ҹ�˾�г����������������������Ƕ�����Ԫ����˵�����ɣ�
���к���һ����ҹ�˾�г����������������������Ƕ�����Ԫ����˵�����ɣ�
���𰸡�(1) ��0��t��30ʱ���г�����������y=2t����30��t��40ʱ���г�����������y=-6t+240����2��t=30��3600.
��������
�����������1����ͼ���֪���г���������y������ʱ��t��0��30��30��40֮�䶼��һ�κ�����ϵ����y=kt+b����ͼ���е�����������뼴�����y��x�Ĺ�ϵ��
��2��Ҫ����������������г�����������ÿ����Ʒ���������������ͼʾ���ֱ��ҳ��г�����������ÿ����Ʒ��������������ֵ���ɣ�
�����������1����ͼ10�ɵã���0��t��30ʱ�����г�����������y=kt��
���㣨30��60����ͼ���ϣ�
��60=30k��
��k=2��y=2t��
��30��t��40ʱ�����г�����������y=k1+t��
![]() �㣨30��60���ͣ�40��0����ͼ���ϣ�
�㣨30��60���ͣ�40��0����ͼ���ϣ�
��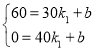 ���k1=-6��b=240��
���k1=-6��b=240��
��y=-6t+240��
���Ͽ�֪����0��t��30ʱ���г�����������y=2t��
��30��t��40ʱ���г�����������y=-6t+240��
��2������һ����ͼ10֪����t=30���죩ʱ���г������������ﵽ���60���������ͼ11֪����t=30���죩ʱ��Ʒ������������ﵽ���60��Ԫ/�������Ե�t=30���죩ʱ���г�������������������ֵΪ3600��Ԫ��
����������ͼ11�ã�
��0��t��20ʱ��ÿ����Ʒ������������Ϊy=3t����20��t��40ʱ��ÿ����Ʒ������������Ϊy=60��
����0��t��20ʱ����Ʒ������������y=3t��2t=6t2��
����t=20ʱ����Ʒ������������y������2400��Ԫ��
����20��t��30ʱ����Ʒ������������y=60��2t=120t��
����t=30ʱ����Ʒ������������y������3600��Ԫ��
����30��t��40ʱ����Ʒ������������y=60��(-6t+240)��
����t=30ʱ����Ʒ������������y������3600��Ԫ��
�ۺ�������������֪����t=30��ʱ����ҹ�˾�г����������������Ϊ3600��Ԫ��
����: һ�κ�����Ӧ�ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��̽�����ɣ��۲�������ʽ��������⣮
1+3 =4 =22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+7+9=25=52;
(1)�����1+3+5+7+9+��+19=
(2)�����1+3+5+7+9+��+��2n-1��+��2n +1��+(2n +3)=
(3)�Լ��㣺101 +103+��+197 +199.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�����˵����ȷ�ĸ����ǣ�����������
����O�ǡ�ABC�����ģ���A=50�㣬���BOC=100�㣻
����O�ǡ�ABC�����ģ���A=50�㣬���BOC=115�㣻
����BC=6��AB+AC=10�����ABC����������ֵ��12��
�ܡ�ABC�������12���ܳ���16����������Բ�İ뾶��1��
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����������Ա��ϰ�۷��ܣ��������߳�������ǰ�������������ؼ������������ļ�¼���£�����λ���ף�+5��-3��+10��-8��-6��+12��-10
��1������Ա����Ƿ�ص��������ߵ�λ�ã�
��2������ϰ�����У�����Ա�뿪������Զ�����Ƕ����ף�
��3������Աȫ����ϰ�������������˶����ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�Ƽ�������˾���Ƴ�һ�����͵IJ�Ʒ��ÿ����Ʒ�ijɱ�Ϊ2400Ԫ�����۵��۶�Ϊ3000Ԫ���ڸò�Ʒ�������ڼ䣬Ϊ�˴����������̼ҹ�������Ͳ�Ʒ����˾�����̼�һ�ι����������Ͳ�Ʒ������10��ʱ��ÿ����3000Ԫ���ۣ���һ�ι�����ֲ�Ʒ����10��ʱ��ÿ���һ�����������ȫ����Ʒ�����۵��۾�����10Ԫ�������۵��۾�������2600Ԫ��
��1���̼�һ�ι������ֲ�Ʒ���ټ�ʱ�����۵���ǡ��Ϊ2600Ԫ��
��2�����̼�һ�ι������ֲ�Ʒx����������˾����õ�����ΪyԪ����y��Ԫ����x������֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3���ù�˾��������Ա���֣����̼�һ�ι����Ʒ�ļ�������ijһ����ʱ�����������һ�ι�������������࣬��˾����õ�����������һ�����Ϊʹ�̼�һ�ι��������Խ�࣬��˾����õ�����Խ��˾Ӧ��������۵��۵���Ϊ����Ԫ�������������������䣩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲����е���ʽ����x��3x2����5x3��7x4��������37x19��39x20������д����n��nΪ��������������ʽ��Ϊ���������⣬���ṩ����Ľ���˼·��
��1�����鵥��ʽ��ϵ���ķ��Ź������� ����ϵ���ľ���ֵ�������� ����
��2�����鵥��ʽ�Ĵ����Ĺ������� ����
��3����������Ĺ��ɣ����Բ����n��nΪ��������������ʽ��
��4��������ݲ��룬д����2017������2018������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
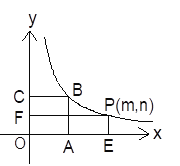
����Ŀ����ͼ����֪������OABC�����Ϊ9����OΪ����ԭ�㣬��A��C�ֱ���x�ᡢy���ϣ���B �ں���![]() (k��0��x��0)��ͼ���ϣ���P (m��n)�Ǻ���
(k��0��x��0)��ͼ���ϣ���P (m��n)�Ǻ���![]() (k��0��x��0)��ͼ��������һ�㣬��P�ֱ���x�ᡢy��Ĵ��ߣ�����ΪE��F�������OEPF��������OABC����IJ��ֵ����ΪS.
(k��0��x��0)��ͼ��������һ�㣬��P�ֱ���x�ᡢy��Ĵ��ߣ�����ΪE��F�������OEPF��������OABC����IJ��ֵ����ΪS.
����B�������k��ֵ��
�ڵ�![]() ʱ�����P�����ꣻ
ʱ�����P�����ꣻ
��д��S����m�ĺ�����ϵʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
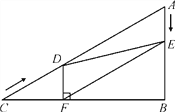
����Ŀ����ͼ����Rt��ABC�У���B��90�㣬AC��60 cm����A��60������D�ӵ�C������CA������4 cm/����ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2 cm/����ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����t��(0<t��15)������D��DF��BC�ڵ�F������DE��EF��
(1)��֤��AE��DF��
(2)�ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ���˵�����ɣ�
(3)��tΪ��ֵʱ����DEFΪֱ�������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��OΪֱ��AB��һ�㣬����O������OC����AOC=30������һֱ�����ǰ壨��M=30������ֱ�Ƕ�����ڵ�O����һ��ON������OA�ϣ���һ��OM��OC����ֱ��AB���Ϸ���
(1)��ͼ1�е����ǰ��Ƶ�O��ÿ��3�����ٶ���˳ʱ�뷽����תһ�ܣ���ͼ2������t���OMǡ��ƽ�֡�BOC����t=�� ����ֱ��д�����
(2)��(1)�ʵĻ����ϣ������ǰ���ת����ͬʱ������OCҲ��O����ÿ��6�����ٶ���˳ʱ�뷽����תһ�ܣ���ͼ3����ô�����������OCƽ�֡�MON����˵�����ɣ�
(3)��(2)�ʵĻ����ϣ���ô�����������MOC=36������˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com