
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A����Ϊ��2��4����ֱ��x=2��x���ཻ�ڵ�B��������y=x2�Ķ�����ֱ��AO���˶�����ֱ��x=2���ڵ�P����ƽ�ƺ�������߶���M�ĺ�����Ϊm��
��1����ͼ1����m=��1�����P�����ꣻ
��2����������ƽ�ƵĹ����У�����PMA�ǵ���������ʱ����m��ֵ��
��3����ͼ2�����߶�BP���ʱ����Ӧ�����������Ƿ���ڵ�Q��ʹ��QMA��������PMA�������ȣ������ڣ��������Q�����ꣻ�������ڣ���˵�����ɣ�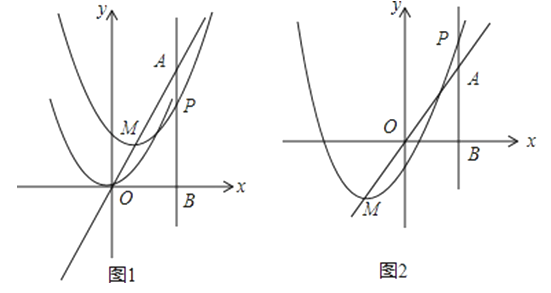
���𰸡��⣺��1����OA����ֱ�ߵĺ�������ʽΪy=kx��
��A��2��4����
��2k=4��
��k=2��
��OA����ֱ�ߵĺ�������ʽΪy=2x��
�����⣬��x=��1������ã�y=��2��
�������ߵĶ���M����1����2����
�������߽���ʽΪ��y=��x+1��2��2=x2+2x��1��
��x=2ʱ��y=7��
���P��2��7����
��2����ͼ1��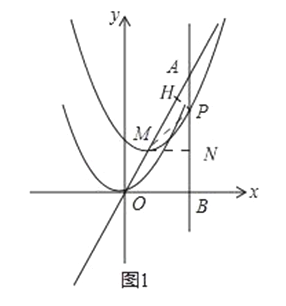
��������ƽ�ƵĹ����У��趥�����꣨m��2m������PMA�ǵ���������ʱ��
����PA=PM��
�ɵ�A��2��4����
����tan��A=![]() ��cos��A=
��cos��A=![]() ��
��
����M��MN��ֱ��ֱ��x=2������P��PH��AM������MP��
�����߽���ʽΪ��y=��x��m��2+2m��
��x=2ʱ��y=m2��2m+4��
��ʱ��MN=2��m��AN=4��2m��
AP=4����m2��2m+4��=��m2+2m��
��AH=AP��![]() =
=![]() ��
��
AM=2AH=![]() ��
��
��![]() =
=![]() ��
��
�����ã�m=![]() ����m=2����ȥ��
����m=2����ȥ��
��m=![]() ��
��
��3����ͼ2��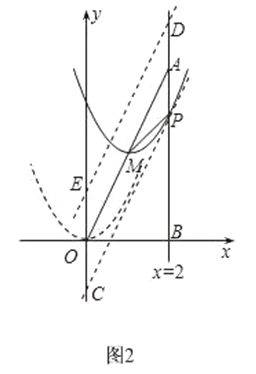
�߶���M�ĺ�����Ϊm������ֱ��OA���ƶ���
��y=2m��
�ඥ��M������Ϊ��m��2m����
�������ߺ�������ʽΪy=��x��m��2+2m��
�൱x=2ʱ��y=��2��m��2+2m=m2��2m+4��
���P�������ǣ�2��m2��2m+4����
��PB=m2��2m+4=��m��1��2+3��
�൱m=1ʱ��PB��̣�
���߶�PB���ʱ����ʱ�����ߵĽ���ʽΪy=��x��1��2+2
��y=x2��2x+3��
�������������ϴ��ڵ�Q��ʹS��QMA=S��PMA ��
���Q��������x��x2��2x+3����
�ٵ�Q����ֱ��OA���·�ʱ����P��ֱ��PC��AO����y���ڵ�C��
��PB=3��AB=4��
��AP=1��
��OC=1��
��C��������ǣ�0����1����
�ߵ�P�������ǣ�2��3����
��ֱ��PC�ĺ�������ʽΪy=2x��1��
��S��QMA=S��PMA ��
���Q����ֱ��y=2x��1�ϣ�
��x2��2x+3=2x��1��
���x1=2��x2=2��
����Q��2��3����
���Q���P�غϣ�
���ʱ�������ϴ��ڵ�Q��2��3����ʹ��QMA���APM�������ȣ�
�ڵ���Q����ֱ��OA���Ϸ�ʱ��
����P���ڵ�A�ĶԳƳƵ�D����D��ֱ��DE��AO����y���ڵ�E��
��AP=1��
��EO=DA=1��
��E��D������ֱ��ǣ�0��1������2��5����
��ֱ��DE��������ʽΪy=2x+1��
��S��QMA=S��PMA ��
���Q����ֱ��y=2x+1�ϣ�
��x2��2x+3=2x+1��
��ã�x=2+![]() ����x=2-
����x=2-![]() ��
��
����y=2x+1���ã�y=5+2![]() ��y=5-2
��y=5-2![]() ��
��
���QMA��������PMA��������ʱ����Q������Ϊ����2+![]() ��5+2
��5+2![]() ������2-
������2-![]() ��5-2
��5-2![]() ����
����
����������1�������ֱ��OA�Ľ���ʽ������m=��1����������ߵĶ������꣬������������߽���ʽ��
��2������M��MN��ֱ��ֱ��x=2������P��PH��AM������MP����������߶������꣬��ʾPA��AM��MN���ij��ȣ���ϡ�A�����Ǻ����г�������⼴�ɣ�
��3�������BP���ʱ�������߽���ʽ�������Q���꣬���������ƽ���ߣ���Q��ֱ��OA���Ϸ����·���������ֱ���ʽ��⼴�ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ABCD�У���E��AD�ϣ�����BE��DF��BE��BC�ڵ�F��AF��BE���ڵ�M��CE��DF���ڵ�N��AF��BE�ֱ�ƽ����BAD����ABC��CE��DF�ֱ�ƽ����BCD����ADC�����ı���MFNE�ǣ�������

A. ���� B. ���� C. ƽ���ı��� D. ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��������һ��һ���ң����������ӵĵ������ϵ�ש������ṹ��ͼ��ʾ������ͼ�����������ݣ���λ���ף�������������⣺
��1���ú� ![]() �Ĵ���ʽ��ʾ����������
�Ĵ���ʽ��ʾ���������� ![]() ��
��

��2����֪ ![]() ���ҿ�������������������
���ҿ������������������� ![]() ���������
��������� ![]() ƽ����ש��ƽ������Ϊ
ƽ����ש��ƽ������Ϊ ![]() Ԫ����ôС���̵�ש���ܷ���Ϊ����Ԫ?
Ԫ����ôС���̵�ש���ܷ���Ϊ����Ԫ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ཫ��һЩƹ�����ƹ�����ģ��˽���Ϣ���£��ס��������̵��������ͬ��Ʒ�Ƶ�ƹ�����ƹ�����ģ�ƹ������ÿ������30Ԫ��ƹ����ÿ�ж���5Ԫ����Ǣ̸����ÿ��һ��������һ��ƹ�����ҵ�ȫ�������۵�9���Żݣ��ð�������5����ƹ�������ɺ�(��С��5��)���ʣ�
(1)������ƹ����x��ʱ�������Żݰ취��Ӧ�������Ԫ��(�ú�x�Ĵ���ʽ��ʾ)
(2)���Ҫ����15��ƹ����ʱ������ȥ������£������ȥ�ļ��̵깺��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����E�ڶԽ���BD�ϣ��ҡ�BAE=22.5�㣬EF��AB������ΪF����EF�ij�Ϊ��������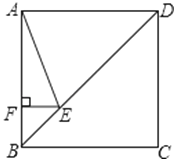
A.1
B.![]()
C.4��2![]()
D.3![]() ��4
��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Сǿ��A�������ر�ƫ��70���������ߣ�����B���������ű�ƫ��30������������C������ʱ��ѷ�������������ʱһ�£�����ĵ���Ӧ�ǣ�������
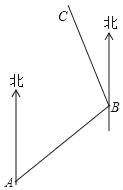
A. ��ת 80�� B. ��ת80�� C. ��ת 100�� D. ��ת 100��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=3cm��BC=6cm.��P�ӵ�D�������A�˶����˶�����A��ֹͣ��ͬʱ����Q�ӵ�B�������C�˶����˶�����C��ֹͣ����P��Q���ٶȶ���1cm/s.����PQ��AQ��CP.���P��Q�˶���ʱ��Ϊts.
��tΪ��ֵʱ���ı���ABQP�Ǿ��Σ�
��tΪ��ֵʱ���ı���AQCP�����Σ�
�ֱ������2��������AQCP���ܳ������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OΪԲ�ĵĻ�BD����Ϊ60�㣬��BOE=45�㣬DA��OB��EB��OB��
��1����![]() ��ֵ��
��ֵ��
��2����OE�뻡BD���ڵ�M��OCƽ����BOE������CM��˵��CMΪ��O�����ߣ���3���ڣ�2���������£���BC=1����tan��BCO��ֵ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com