
【题目】如图,在△ABC中,∠A=90°,O是BC边上一点,以O为圆心的半圆分别与AB、AC边相切于D、E两点,连接OD.已知BD=2,AD=3.求: 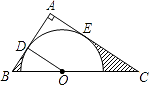
(1)tanC;
(2)图中两部分阴影面积的和.
【答案】
(1)解:连接OE,
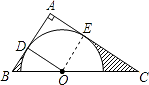
∵AB、AC分别切⊙O于D、E两点,
∴AD⊥OD,AE⊥OE,
∴∠ADO=∠AEO=90°,
又∵∠A=90°,
∴四边形ADOE是矩形,
∵OD=OE,
∴四边形ADOE是正方形,
∴OD∥AC,OD=AD=3,
∴∠BOD=∠C,
∴在Rt△BOD中, ![]() ,
,
∴ ![]() .
.
答:tanC= ![]()
(2)解:如图,设⊙O与BC交于M、N两点,
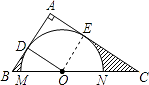
由(1)得:四边形ADOE是正方形,
∴∠DOE=90°,
∴∠COE+∠BOD=90°,
∵在Rt△EOC中, ![]() =
= ![]() ,OE=3,
,OE=3,
∴ ![]() ,
,
∴S扇形DOM+S扇形EON=S扇形DOE= ![]() ,
,
∴S阴影=S△BOD+S△COE﹣(S扇形DOM+S扇形EON)= ![]() ,
,
答:图中两部分阴影面积的和为 ![]() .
.
【解析】(1)连接OE,得到∠ADO=∠AEO=90°,根据∠A=90°,推出矩形ADOE,进一步推出正方形ADOE,得出OD∥AC,OD=AD=3,∠BOD=∠C,即可求出答案;(2)设⊙O与BC交于M、N两点,由(1)得:四边形ADOE是正方形,推出∠COE+∠BOD=90°,根据 ![]() ,OE=3,求出
,OE=3,求出 ![]() ,根据S扇形DOM+S扇形EON=S扇形DOE , 即可求出阴影部分的面积.
,根据S扇形DOM+S扇形EON=S扇形DOE , 即可求出阴影部分的面积.


科目:初中数学 来源: 题型:
【题目】小华和小容都想参加学校组织的数学兴趣小组,根据学校分配的名额,他们两人只能有1人参加.数学老师想出了一个主意:如图,给他们六张卡片,每张卡片上都有一些数,将化简后的数在数轴上表示出来,再用“<”连接起来,谁先按照要求做对,谁就参加兴趣小组,你也一起来试一试吧!
-(-2) (-1)3 -|-3| 0的相反数
① ② ③ ④
-0.4的倒数 比-1大2.5的数
⑤ ⑥
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村庄计划建造A,B两种型号的沼气池共20个,以解决该村所有农户的燃料问题.两种型号沼气池的占地面积和可供使用农户数见下表:
型号 | 占地面积 (单位:m2/个) | 可供使用农户数 (单位:户/个) |
A | 15 | 18 |
B | 20 | 30 |
已知可供建造沼气池的占地面积不超过365m2,该村农户共有492户.
(1)如何合理分配建造A,B型号“沼气池”的个数才能满足条件?满足条件的方案有几种?通过计算分别写出各种方案.
(2)请写出建造A、B两种型号的“沼气池”的总费用y和建造A型“沼气池”个数x之间的函数关系式;
(3)若A型号“沼气池”每个造价2万元,B型号“沼气池”每个造价3万元,试说明在(1)中的各种建造方案中,哪种建造方案最省钱,最少的费用需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某七年级的同学就“别人帮助你时,你是否会道一声谢谢”这个问题对本班级66名同学进行了调查,调查结果如下:
是 是 是 有时 是 是 是 否 是 有时 有时 是 是 有时 有时 是 是 有时 是 是 有时 有时 是 有时 是 是 有时 有时 有时 是 是 是 有时 有时 否 否 有时 有时 是 是 否 是 是 是 否 是 是 是 是 是 是 是 是 有时 是 否 是 是 是 是 否 否 否 是 否 是
(1)请用统计表整理上述数据,百分比的结果精确到整数.
回答内容 | 划记 | 人数 | 百分比 |
是 | |||
有时 | |||
否 |
(2)通过对这组数据的分析,你有何感想?用一句话表示即可.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕顶点C逆时针旋转得到△A′B′C′,且点B刚好落在A′B′上,若∠A=25°,∠BCA′=45°,则∠A′BA等于( )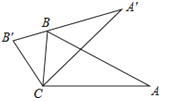
A.30°
B.35°
C.40°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是( )

A. 菱形 B. 矩形 C. 平行四边形 D. 正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,对角线AC,BD相交于点O.
(1)如图1,点P是正方形ABCD外一点,连接OP,以OP为一边,作正方形OPMN,且边ON与边BC相交,连接AP,BN.
①依题意补全图1;
②判断AP与BN的数量关系及位置关系,写出结论并加以证明;
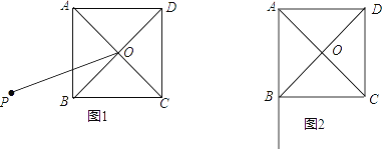
(2)点P在AB延长线上,且∠APO=30°,连接OP,以OP为一边,作正方形OPMN,且边ON与BC的延长线恰交于点N,连接CM,若AB=2,求CM的长(不必写出计算结果,简述求CM长的过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王购买了一套一居室,他准备将房子的地面铺上地砖,地面结构如图所示,根据图中所给的数据(单位:米),解答下列问题:
(1)用含 ![]() 的代数式表示地面的总面积
的代数式表示地面的总面积 ![]() ;
;

(2)已知 ![]() ,且客厅面积是卫生间面积的
,且客厅面积是卫生间面积的 ![]() 倍,如果铺
倍,如果铺 ![]() 平方米地砖的平均费用为
平方米地砖的平均费用为 ![]() 元,那么小王铺地砖的总费用为多少元?
元,那么小王铺地砖的总费用为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com