
【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.

(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
【答案】(1)8﹣2t;2+t;(2)2;(3)①存在时刻t=1,使四边形AQMK为菱形.理由详见解析;②8![]() .
.
【解析】试题分析:(1)由DM=2t,根据AM=AD-DM即可求出AM=6-2t;先证明四边形CNPD为矩形,得出DP=CN=4-t,则AP=AD-DP=2+t;
(2)根据四边形ANCP为平行四边形时,可得4-t=6-(6=4-t),解方程即可;
(3))①由NP⊥AD,QP=PK,可得当PM=PA时有四边形AQMK为菱形,列出方程4-t-2t=6-(4-t),求解即可,
②要使四边形AQMK为正方形,由∠ADC=90°,可得∠CAD=45°,所以四边形AQMK为正方形,则CD=AD,由AD=8,可得CD=6,利用勾股定理求得AC即可.
试题解析:(1)6﹣2t,2+t.
(2)∵四边形ANCP为平行四边形时,CN=AP,
∴4﹣t=t+2,解得t=1,
(3)①∵NP⊥AD,QP=PK,
∴当PM=PA时有四边形AQMK为菱形,
∴4﹣t﹣2t=2+t,解得t=0.5,
∴存在时刻t=0.5,使四边形AQMK为菱形.
②AC=6![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
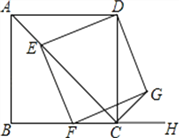
【题目】如图,已知四边形ABCD为正方形,AB=![]() ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB、BC上,且AE=BF=1,CE、DF交于点O.下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD= ![]() ,④S△ODC=S四边形BEOF中,正确的有( )
,④S△ODC=S四边形BEOF中,正确的有( ) 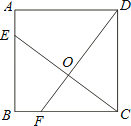
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暴雨过后,某地遭遇山体滑坡,武警总队派出一队武警战士前往抢险.半小时后,第二队前去支援,平均速度是第一队的1.5倍,结果两队同时到达.已知抢险队的出发地与灾区的距离为90千米,两队所行路线相同.
(1)问两队的平均速度分别是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某三岔路口交通环岛的简化模型,在某高峰时刻,单位时间进出路口A,B,C的机动车辆数如图所示.图中x1,x2,x3分别表示该时段单位时间通过路段AB,BC,CA的机动车辆数(假设单位时间内在上述路段中同一路段上驶入与驶出的车辆数相等),则有( )

A. x1>x2>x3 B. x1>x3>x2 C. x2>x3>x1 D. x3>x2>x1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车间有120名工人,为了了解这些工人日加工零件数的情况,随机抽出其中的30名工人进行调查.整理调查结果,绘制出不完整的条形统计图(如图).根据图中的信息,解答下列问题:
(1)在被调查的工人中,日加工9个零件的人数为名;
(2)在被调查的工人中,日加工12个零件的人数为名,日加工个零件的人数最多,日加工15个零件的人数占被调查人数的%;
(3)依据本次调查结果,估计该车间日人均加工零件数和日加工零件的总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为( )
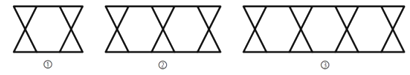
A. 12 B. 14 C. 16 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽一家利用元旦三天驾车到某景点旅游.小汽车出发前油箱有油36L,行驶ah后,途中在加油站加油若干bL.油箱中余油量Q(L)与行驶时间t(h)之间的关系如图所示.根据图象回答下列问题:
①小汽车行驶________h后加油, 中途加油__________L;
②求加油前油箱余油量Q与行驶时间t的函数关系式;
③如果加油站距景点200km,车速为80km/h,要到达目的
地,油箱中的油是否够用?请说明理由。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com