
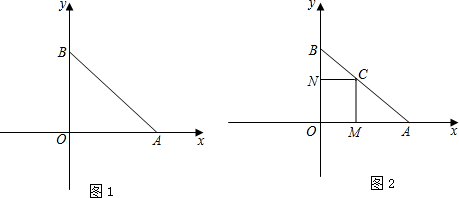
���� ��1���ɷǸ��������ʵõ�����a-b=0��2a+b-6=0������ȡ�ý����
��2�����ڣ���P��m��0������S��PAB=3S��OAB���з���$\frac{1}{2}|2-m|��2=3��\frac{1}{2}��2��2$����ý����
��3��CM+CNΪ��ֵ��������֪�õ�CN��OA��CM��OB���˳���BCN�ס�ACM�ס�AOB���õ�����ʽ$\frac{CN}{OA}=\frac{BC}{AB}$��$\frac{CM}{OB}=\frac{AC}{AB}$������$\frac{CN}{2}+\frac{CM}{2}=\frac{CB}{AB}+\frac{AC}{AB}=\frac{AB}{AB}$=1�����ɵõ�CM+CN=2Ϊ��ֵ��
��� �⣺�ߣ�1��$\sqrt{a-b}$+|2a+b-6|=0��
��a-b=0��2a+b-6=0��
��ã�a=2��b=2��
��A��2��0����B��0��2����
��2�����ڣ�
��P��m��0����
��S��PAB=3S��OAB��
��$\frac{1}{2}$PA•OB=3��$\frac{1}{2}$OA•OB��
����$\frac{1}{2}|2-m|��2=3��\frac{1}{2}��2��2$��
��ã�m=-4��m=8��
��P��-4��0����P��8��0����
��3��CM+CNΪ��ֵ��
��CM��OA��M��CN��OB��N��
���AOB=��CNO=��CMO=90�㣬
���ı���CNOM�Ǿ��Σ�
��CN��OA��CM��OB��
���BCN�ס�ACM�ס�AOB��
��$\frac{CN}{OA}=\frac{BC}{AB}$��$\frac{CM}{OB}=\frac{AC}{AB}$��
��$\frac{CN}{2}+\frac{CM}{2}=\frac{CB}{AB}+\frac{AC}{AB}=\frac{AB}{AB}$=1��
��CN+CM=2��
��CM+CNΪ��ֵ��
���� ���⿼����������ͼ�ε����ʣ������ε���������ε����ʣ����������ε��ж������ʣ��������ո����ʶ����ǽ���Ĺؼ���


 ��������ѧ����ϵ�д�
��������ѧ����ϵ�д� ��Ԫ������ĩ��ϵ�д�
��Ԫ������ĩ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �����ܷ��� | B�� | ��Ȼ���� | C�� | �ܿ��ܷ��� | D�� | ��̫���ܷ��� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
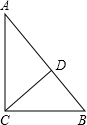 ��ͼ��CD��AB�ϵĸߣ�AC=4��BC=3��DB=$\frac{9}{5}$��
��ͼ��CD��AB�ϵĸߣ�AC=4��BC=3��DB=$\frac{9}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��0 | B�� | a��1 | C�� | a��1 | D�� | 0��a��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
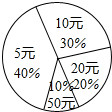 «ɽ��������ij��50��ͬѧ��ӦѧУ���٣�����㻨Ǯ����������ͼ��ʾ����ð���700Ԫ��
«ɽ��������ij��50��ͬѧ��ӦѧУ���٣�����㻨Ǯ����������ͼ��ʾ����ð���700Ԫ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5��25������ƽ���� | B�� | -1��1��һ��ƽ���� | ||
| C�� | ��-4��2������ƽ������-4 | D�� | 0��ƽ������0 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4��1 | B�� | 1��2 | C�� | 2��1 | D�� | 1��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com