
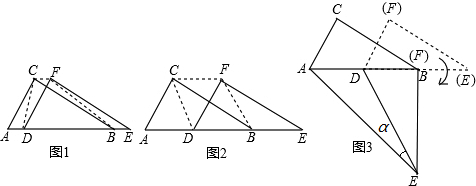
分析 (1)如图1,先利用平移的性质得CF=AD,AC=DF,则可判断四边形ACFD为平行四边形,利用三角形面积公式得到S△DCF=S△BCF=S△ACD,则S四边形CDBF=S△ACB,然后计算S△ABC即可;
(2)如图2,利用直角三角形斜边上的中线性质得DC=DA=DB,则可证明四边形CDBF为平行四边形,于是可判断四边形CDBF为菱形;
(3)作DH⊥AE于H,如图,先计算出AB=2AC=2,则AD=BD=$\frac{1}{2}$AB=1,再利用旋转的性质得∠EFD=90°,EB=$\sqrt{3}$,DE=AB=2,接着利用勾股定理计算出AE=$\sqrt{7}$,然后利用面积法可计算出DH=$\frac{\sqrt{21}}{7}$,再在Rt△EDH中利用正弦的定义求sinα的值.
解答 解:(1)如图1,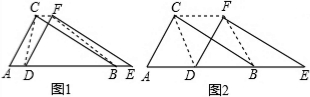 ∵△DEF沿线段AB向右平移(即D点在线段AB内移动),
∵△DEF沿线段AB向右平移(即D点在线段AB内移动),
∴CF=AD,AC=DF,
∴四边形ACFD为平行四边形,
∴AD∥CF,
∴S△DCF=S△BCF=S△ACD,
∴S四边形CDBF=S△CDB+S△BCF=S△CDB+S△ACD=S△ACB,
在Rt△ACB中,∵∠A=60°,
∴BC=$\sqrt{3}$AC=$\sqrt{3}$,
∴S△ABC=$\frac{1}{2}$×1×$\sqrt{3}$=$\frac{\sqrt{3}}{2}$,
∴S四边形CDBF=$\frac{\sqrt{3}}{2}$;
(2)四边形CDBF为菱形.理由如下:
如图2,∵点D为斜边AB的中点,
∴DC=DA=DB,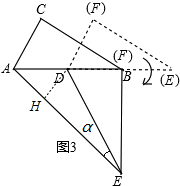
∵CF∥AD,CF=AD,
∴CF=BD,CF∥DB,
∴四边形CDBF为平行四边形,
而DC=DB,
∴四边形CDBF为菱形;
(3)作DH⊥AE于H,如图,
在Rt△ACB中,∵∠A=60°,
∴AB=2AC=2,
∵点D为AB的中点,
∴AD=BD=$\frac{1}{2}$AB=1,
∵绕D点按顺时针方向旋转△DEF,使DF落在AB边上,此时F点恰好与B点重合,
∴∠EFD=90°,EB=$\sqrt{3}$,DE=AB=2,
在Rt△ABE中,AE=$\sqrt{B{E}^{2}+A{B}^{2}}$=$\sqrt{(\sqrt{3})^{2}+{2}^{2}}$=$\sqrt{7}$,
∵$\frac{1}{2}$DH•AB=$\frac{1}{2}$AD•EB,
∴DH=$\frac{1×\sqrt{3}}{\sqrt{7}}$=$\frac{\sqrt{21}}{7}$,
在Rt△EDH中,sinα=$\frac{DH}{DE}$=$\frac{\sqrt{21}}{14}$.
故答案为$\frac{\sqrt{21}}{14}$.
点评 本题考查四边形综合题、平移、旋转的性质和菱形的判定方法、平行线的性质、锐角三角函数、直角三角形30度角性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题


科目:初中数学 来源: 题型:解答题
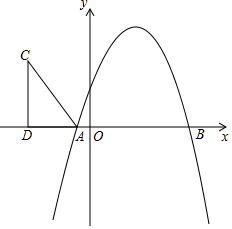 如图,抛物线y=-x2+bx+c与x轴分别交于A(-1,0),B(5,0)两点.
如图,抛物线y=-x2+bx+c与x轴分别交于A(-1,0),B(5,0)两点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
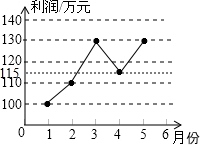 某企业1-5月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是( )
某企业1-5月份利润的变化情况如图所示,以下说法与图中反映的信息相符的是( )| A. | 1-5月份利润的众数是130万元 | |
| B. | 1-4月份利润的极差与1-5月份利润的极差不同 | |
| C. | 1-2月份利润的增长快于2-3月份利润的增长 | |
| D. | 1-5月份利润的中位数是130万元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 城市 | 吐鲁番 | 乌鲁木齐 | 喀什 | 阿勒泰 |
| 气温(℃) | -8 | -16 | -5 | -25 |
| A. | 吐鲁番 | B. | 乌鲁木齐 | C. | 喀什 | D. | 阿勒泰 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.
如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A($\sqrt{3}$,1)在反比例函数y=$\frac{k}{x}$的图象上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
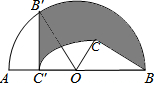 如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为πcm2.
如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为πcm2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com