
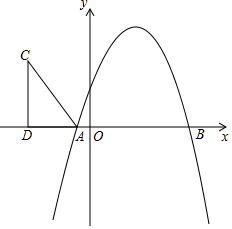
 ��ͼ��������y=-x2+bx+c��x��ֱ���A��-1��0����B��5��0�����㣮
��ͼ��������y=-x2+bx+c��x��ֱ���A��-1��0����B��5��0�����㣮���� ��1����A��B�����꣬���ô���ϵ��������������ߵĽ���ʽ��
��2������������C�����꣬��ƽ�ƺ�ĵ�C�Ķ�Ӧ��ΪC�䣬��C����������Ϊ8�����������߽���ʽ�����C�������꣬������ƽ�Ƶĵ�λ�������m��ֵ��
��3���ɣ�2�������E�����꣬����BE���Գ����ڵ�M����E��EF��x���ڵ�F����BEΪƽ���ı��εı�ʱ����Q���Գ���Ĵ��ߣ�����ΪN�����֤�á�PQN�ա�EFB�������QN���������Q���Գ���ľ��룬������Q��ĺ����꣬���������߽���ʽ�����Q�����ꣻ��BEΪ�Խ���ʱ����B��E�����������߶�BE���е����꣬��Q��x��y������P��ĺ�����������Q��ĺ����꣬���������߽���ʽ�����Q������꣮
��� �⣺
��1����������y=-x2+bx+c��x��ֱ���A��-1��0����B��5��0�����㣬
��$\left\{\begin{array}{l}{-1-b+c=0}\\{-25+5b+c=0}\end{array}\right.$�����$\left\{\begin{array}{l}{b=4}\\{c=5}\end{array}\right.$��
�������߽���ʽΪy=-x2+4x+5��
��2����AD=5����OA=1��
��OD=6����CD=8��
��C��-6��8����
��ƽ�ƺ�ĵ�C�Ķ�Ӧ��ΪC�䣬��C����������Ϊ8��
���������߽���ʽ�ɵ�8=-x2+4x+5�����x=1��x=3��
��C����������1��8����3��8����
��C��-6��8����
�൱��C������������ʱ������ƽ����7��9����λ��
��m��ֵΪ7��9��
��3����y=-x2+4x+5=-��x-2��2+9��
�������߶Գ���Ϊx=2��
�����P��2��t����
�ɣ�2����֪E������Ϊ��1��8����
�ٵ�BEΪƽ���ı��εı�ʱ������BE���Գ����ڵ�M����E��EF��x���ڵ�F����Q���Գ���Ĵ��ߣ�����ΪN����ͼ��
���BEF=��BMP=��QPN��
�ڡ�PQN�͡�EFB��
$\left\{\begin{array}{l}{��QPN=��BEF}\\{��PNQ=��EFB}\\{PQ=BE}\end{array}\right.$
���PQN�ա�EFB��AAS����
��NQ=BF=OB-OF=5-1=4��
��Q��x��y������QN=|x-2|��
��|x-2|=4�����x=-2��x=6��
��x=-2��x=6ʱ�����������߽���ʽ�����y=-7��
��Q��������-2��-7����6��-7����
�ڵ�BEΪ�Խ���ʱ��
��B��5��0����E��1��8����
���߶�BE���е�����Ϊ��3��4�������߶�PQ���е�����Ϊ��3��4����
��Q��x��y������P��2��t����
��x+2=3��2�����x=4����x=4���������߽���ʽ�����y=5��
��Q��4��5����
���Ͽ�֪Q�������Ϊ��-2��-7����6��-7����4��5����
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰����ϵ������ƽ�Ƶ����ʡ�ȫ�������ε��ж������ʡ�ƽ���ı��ε����ʡ�����˼�뼰��������˼���֪ʶ���ڣ�1��ע�����ϵ������Ӧ�ã��ڣ�2�������ƽ�ƺ�C��Ķ�Ӧ��������ǽ���Ĺؼ����ڣ�3����ȷ����Q���λ���ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | ��첻��ʤ�����䣬���Ժ��ʤ�ĸ���Ϊ$\frac{1}{2}$ | |
| B�� | ���ʤ������ʤ�ĸ������ | |
| C�� | ���˳���ͬ���Ƶĸ���Ϊ$\frac{1}{3}$ | |
| D�� | ����ʤ�ĸ��ʺ����˳���ͬ���Ƶĸ���һ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
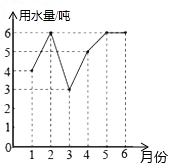 С����1��6�·ݵ���ˮ��ͳ����ͼ��ʾ�������������ݣ�����˵���д���ģ�������
С����1��6�·ݵ���ˮ��ͳ����ͼ��ʾ�������������ݣ�����˵���д���ģ�������| A�� | ������6�� | B�� | ƽ������5�� | C�� | ��λ����5�� | D�� | ������$\frac{4}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����������ȵ�ʵ���� | B�� | ��������ȵ�ʵ���� | ||
| C�� | û��ʵ���� | D�� | ���ж� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
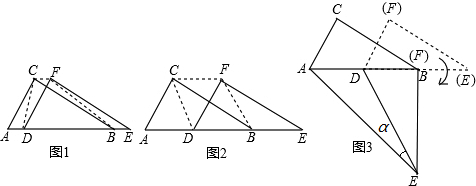
 ��ͼ����O���ڽ��������ABCDE�ĶԽ���AD��BE�ཻ�ڵ�G��AE=2����EG�ij���$\sqrt{5}$-1��
��ͼ����O���ڽ��������ABCDE�ĶԽ���AD��BE�ཻ�ڵ�G��AE=2����EG�ij���$\sqrt{5}$-1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�� | B�� | 1�� | C�� | 2�� | D�� | 3�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2a-3a=a | B�� | ��a3��2=a6 | C�� | $\sqrt{-2a}$=$\sqrt{-2}$��$\sqrt{a}$ | D�� | a6��a3=a2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com