
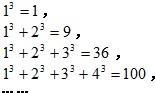
分析 观察发现,等式的左边是连续整数的立方和;右边是连续整数的和的平方.
(1)由于1+2+3+4+5=15,所以13+23+33+43+53=152;
(2)由于1+2+3+4+…+n=$\frac{1}{2}$n(n+1),所以13+23+33+…+n3=[$\frac{1}{2}$n(n+1)]2;
(3)由于1+2+3+4+5+6+7+8+9+10=55,所以13+23+33+43+53+63+73+83+93+103=552.
解答 解:(1)∵13=1,1=1,
13+23=9,1+2=3,
13+23+33=36,1+2+3=6,
13+23+33+43=100,1+2+3+4=10,
┅┅
∴13+23+33+43+53=(1+2+3+4+5)2=152=225;
(2)由(1)的结论得,13+23+33+…+n3=(1+2+3+4+…+n)2=[$\frac{1}{2}$n(n+1)]2;
(3)13+23+33+43+53+63+73+83+93+103=(1+2+3+4+5+6+7+8+9+10)2=552=3025.
点评 本题考查了规律型:数字的变化类,难度适中.注意找等式的规律时,要观察等式的左边和右边的规律,还要注意观察等式的左右两边之间的关系.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
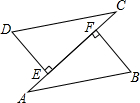 如图所示,已知AB=CD,DE⊥AC,BF⊥AC,E、F为垂足,DE=BF,试说明AE与CF相等.
如图所示,已知AB=CD,DE⊥AC,BF⊥AC,E、F为垂足,DE=BF,试说明AE与CF相等.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com