Question

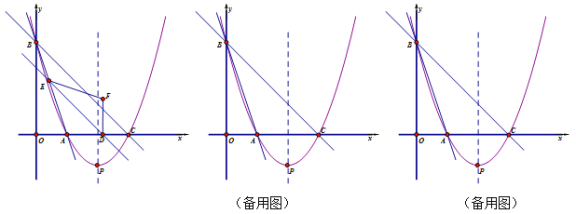
【题目】如图，直线y=﹣3x+3与x轴、y轴分别交于点A、B，对称轴为直线x=2的抛物线经过点A、B，并与x轴交于另一点C，其顶点为P．

（1）求抛物线的解析式；

（2）抛物线的对称轴上有一点Q，使△ABQ是以AB为底边的等腰三角形，求Q点的坐标；

（3）在直线BC的下方的抛物线上有一动点M，其横坐标为m，△MBC的面积为S，求S关于m的函数关系式，并求S的最大值及此时点M的坐标；

（4）平行于BC的动直线分别交△ABC的边AC、AB与点D、E，将△ADE沿DE翻折，得到△FDE，设DE=x，△FDE与△ABC重叠部分的面积为y，直接写出y与x的函数关系式及自变量x的取值范围．

Answer 1

【答案】（1）y=（2）（2，2）；（3）（）（4）y=

【解析】

试题分析：（1）先求出直线y=-3x+3与x轴交点A，与y轴交点B的坐标，再将A、B两点坐标代入y=a（x-2）2+k，得到关于a，k的二元一次方程组，解方程组即可求解；

（2）设Q点的坐标为（2，m），对称轴x=2交x轴于点F，过点B作BE垂直于直线x=2于点E．在Rt△AQF与Rt△BQE中，用勾股定理分别表示出AQ2=AF2+QF2=1+m2，BQ2=BE2+EQ2=4+2，由AQ=BQ，得到方程1+m2=4+2，解方程求出m=2，即可求得Q点的坐标；

（3）当点N在对称轴上时，由NC与AC不垂直，得出AC为正方形的对角线，根据抛物线的对称性及正方形的性质，得到M点与顶点P（2，-1）重合，N点为点P关于x轴的对称点，此时，MF=NF=AF=CF=1，且AC⊥MN，则四边形AMCN为正方形，在Rt△AFN中根据勾股定理即可求出正方形的边长．

（4）根据三角形的面积和相似三角形的性质，根据不同的范围可列函数的解析式.

试题解析：（1）∵直线y=﹣3x+3与x轴、y轴分别交于点A、B，∴A（1，0），B（0，3）．

又∵抛物线的对称轴为直线x=2，∴抛物线与x轴的另一个交点C的坐标为（3，0），

设抛物线的解析式为y=a(x-1)(x-3)，∵抛物线经过点B（0，3），

∴3a=3，解得a=1，故抛物线的解析式为y=；

（2）设Q点的坐标为（2，e），对称轴x=2交x轴于点T，过点B作BR垂直于直线x=2于点R．在Rt△AQT中，AQ2=AT2+QT2=1+e2，在Rt△BQR中，BQ2=BR2+RQ2=4+（3﹣e）2，

∵AQ=BQ，∴1+e2=4+（3﹣e）2，∴e=2，∴Q点的坐标为（2，2）；

（3）过点M作MN∥y轴交直线BC于点N，，M（m，）（0﹤m﹤3）,

N(m，-m+3)，MN=-m+3-（）=，∴S=，当m=，此时M（）.

⑷依题意得△CBA面积为3，BC=.当点F在BC上时，AF⊥BC，且AF=，此时x=DE=，所以分种情况考虑，①当0＜x≤时，△ADE≌△FDE，△ADE∽△ACB，而，计算得．②当＜x＜时，连结AF交ED于K、交BC于G，EF交BC于H，DF交BC于I，由△ADE∽△ACB求得FK＝AK＝，FG＝，再由△FHI∽△FED得，∴．

∴y=

综上所述，函数关系式为y=