
【题目】如图,在梯形ABCD中,AB∥CD.
(1)已知∠A=∠B,求证:AD=BC;
(2)已知AD=BC,求证:∠A=∠B.

【答案】(1)详见解析;(2)详见解析.
【解析】
(1)过C作CE∥DA,可证明四边形ADCE是平行四边形,根据平行四边形的性质可得AD=EC,根据DA∥CE,可得∠A=∠CEB,根据等量代换可得∠CEB=∠B,进而得到EC=BC,从而可得AD=BC;
(2)根据CE∥DA,AB∥CD,可证明四边形AECD是平行四边形,根据平行四边形的性质可得AD=EC,再由条件AD=BC可得EC=BC,根据等边对等角可得∠B=∠CEB,再根据平行线的性质可得∠A=∠CEB,利用等量代换可得∠B=∠A.
解:(1)如图,过点C作CE∥DA,交AB于点E
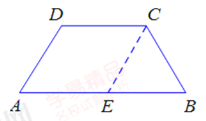
∵CE∥DA,AB∥CD
∴四边形AECD是平行四边形
∴AD=EC
又∵CE∥DA
∴∠A=∠CEB
又∵∠A=∠B
∴∠CEB=∠B
∴EC=BC
∴AD=BC
(2)∵CE∥DA,AB∥CD
∴四边形AECD是平行四边形
∴AD=EC
又∵AD=BC
∴EC=BC
∴∠CEB=∠B
又∵CE∥DA
∴∠CEB=∠A
∴∠B=∠A


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O的直径,点E在⊙O上,∠EAB的平分线交⊙O于点C,过点C作AE的垂线,垂足为D,直线DC与AB的延长线交于点P.
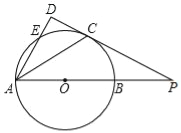
(1)判断直线PC与⊙O的位置关系,并说明理由;
(2)若tan∠P=![]() ,AD=6,求线段AE的长.
,AD=6,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和
(﹣2,0)之间,其部分图象如下图,则以下结论:①b2﹣4ac<0;②a+b+c<0;③c﹣a=2;④方程ax2+bx+c﹣2=0有两个相等的实数根.其中正确结论的个数为( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表给出了1班6名学生的身高情况与全班平均身高的差值(单位:厘米)
学生 | A | B | C | D | E | F |
身高 | 157 | 162 | 159 | 152 | 163 | 164 |
身高与全班平均身高的差值 | -3 | +2 | -1 | a | +3 | b |
(1)列式计算表中数据a和b
(2)这6名学生的平均身高与全班学生的平均身高相比,在数值上有什么关系?(通过计算回答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备购买A、B两种型号篮球,询问了甲、乙两间学校了解这两款篮球的价格,下表是甲、乙两间学校购买A、B两种型号篮球的情况:
购买学校 | 购买型号及数量(个) | 购买支出款项(元) | |
A | B | ||
甲 | 3 | 8 | 622 |
乙 | 5 | 4 | 402 |
(1)求A、B两种型号的篮球的销售单价;
(2)若该学校准备用不多于1000元的金额购买这两种型号的篮球共20个,求A种型号的篮球最少能采购多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产自行车100辆,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的车辆数记为正数,减少的车辆数记为负数):

(1)生产量最多的一天比生产量最少的一天多生产多少辆?
(2)本周总的生产量是多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表是某校九年级(1)班20名学生某次数学测验的成绩统计表:
成绩(分) | 60 | 70 | 80 | 90 | 100 |
人数(人) | 1 | 5 | x | y | 2 |
(1)若这20名学生成绩的平均分数为82分,求x和y的值;
(2)在(1)的条件下,设这20名学生本次测验成绩的众数为a,中位数为b,求a,b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习绝对值后,我们知道,![]() 表示数
表示数![]() 在数轴上的对应点与原点的距离. 如:
在数轴上的对应点与原点的距离. 如:![]() 表示5在数轴上的对应点到原点的距离.而
表示5在数轴上的对应点到原点的距离.而![]() ,即
,即![]() 表示5、0在数轴上对应的两点之间的距离.类似的,有:
表示5、0在数轴上对应的两点之间的距离.类似的,有:![]() 表示5、3在数轴上对应的两点之间的距离;
表示5、3在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示5、
表示5、![]() 在数轴上对应的两点之间的距离. 一般地,点A、B在数轴上分别表示有理数
在数轴上对应的两点之间的距离. 一般地,点A、B在数轴上分别表示有理数![]() 、
、![]() ,那么A、B之间的距离可表示为
,那么A、B之间的距离可表示为![]() .
.
请根据绝对值的意义并结合数轴解答下列问题:
(1)数轴上表示2和5的两点之间的距离是______;数轴上表示1和-3的两点之间的距离是 ;
(2)数轴上P、Q两点的距离为3,且点P表示的数是2,则点Q表示的数是___________.
(3)点A、B、C在数轴上分别表示有理数![]() 、
、![]() 、1,那么A到B的距离与A到C的距离之和可表示为 ;
、1,那么A到B的距离与A到C的距离之和可表示为 ;
(4)满足![]() 的整数
的整数![]() 的值为 .
的值为 .
(5)![]() 的最小值为 .
的最小值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com