Question

【题目】（1）如图1，为正方形的边上一点，将正方形沿折叠,点落在点处，连接并延长，交于点，求证：；

（2）如图2，点分别在边上，且，求证：

（3）如图3，点分别在边上，点分别在边上，交于点，已知，，，求的长.

Answer 1

【答案】（1）见解析；（2）见解析；（3）MN=2 .

【解析】

(1) 连接AF，根据正方形的性质和折叠性质可证明Rt△AGF≌Rt△ADF（HL），从而求得结果DF=GF；（2）属于半角型问题，延长CD至点K，使DK=BE，连接AK，再根据正方形的性质证明△ABE≌△ADK（SAS）和△AFE≌△AFK（SAS）即可解答，具体过程见详解；（3）过点A作AE∥MN交BC于点E，作AF∥PQ交CD于点F，目的是平移MN、PQ到直角三角形中，在Rt△ADF中，AD=6，由勾股定理得DF=3，设BE=x，则CE=6-x，EF=3+x，

在△CEF中，由勾股定理得32+(6-x)2=(3+x)2，从而求解.

（1）连接AF，

∵四边形ABCD是正方形，

∴∠BAD=∠B=∠C=∠D=90°，AB=BC=CD=DA，

由折叠可知，∠AGF=∠AGE=∠ABC=90°，AG=AB=AD，

在Rt△AGF和Rt△ADF中

∵ ，

∴Rt△AGF≌Rt△ADF，

∴DF=GF；

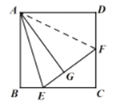
（2）延长CD至点K，使DK=BE，连接AK，

在△ABE和△ADK中

∵ ，

∴△ABE≌△ADK，

∴AE=AK，∠EAB=∠KAD，

∴∠KAE=∠BAD=90°，

∵∠EAF=45°，

∴∠KAF=45°=∠EAF，

在△AFE和△AFK中

∵ ，

∴△AFE≌△AFK，

∴EF=FK=FD+DK=FD+BE；

（3）过点A作AE∥MN交BC于点E，作AF∥PQ交CD于点F，

则∠EAF=∠MOQ=45°，

由（2）可知EF=BE+DF,

∵AN∥EM，AE∥MN，

∴四边形AEMN为平行四边形，

∴AE=MN，

同理AF=PQ=，

在Rt△ADF中，AD=6，由勾股定理得DF=3，

设BE=x，则CE=6-x，EF=3+x，

在△CEF中，由勾股定理得32+(6-x)2=(3+x)2，

解得，x=2，

再由勾股定理得MN=AE=.