
【题目】正方形ABCD中,点M是直线BC上的一个动点(不与点B,C重合),作射线DM,过点B作BN⊥DM于点N,连接CN.
(1)如图1,当点M在BC上时,如果∠CDM=25°,那么∠MBN的度数是 .
(2)如图2,当点M在BC的延长线上时,
①依题意补全图2;
②用等式表示线段NB,NC和ND之间的数量关系,并证明.

【答案】(1)![]() ;(2)①见解析;②
;(2)①见解析;②![]() ,见解析.
,见解析.
【解析】
(1)由正方形的性质和对顶角相等、三角形内角和定理得出∠MBN=∠CDM=25°即可;
(2)①由题意补全图形即可;
②当N在DM上时,在NB上截取BE=ND,证明△CDN≌△CBE得出NC=EC,∠DCN=∠BCE,证出∠NCE=∠BCD=90°,得出△NCE是等腰直角三角形,得出NE=![]() NC,即可得出结论;
NC,即可得出结论;
当N在MD延长线上时,延长NB至E,使BE=ND,同理得:△CDN≌△CBE,得出NC=EC,∠DCN=∠BCE,证出∠NCE=∠BCD=90°,得出△NCE是等腰直角三角形,证出NE=![]() NC,即可得出结论.
NC,即可得出结论.
解:(1)∵四边形ABCD是正方形,
∴BC=CD,∠DCM=∠BCD=90°,
∵BN⊥DM,
∴∠DNB=90°=∠BCD,
∵∠BMN=∠DMC,
∴∠MBN=∠CDM=25°;
故答案为:25°;
(2)①由题意补全图形如图2、图4所示;
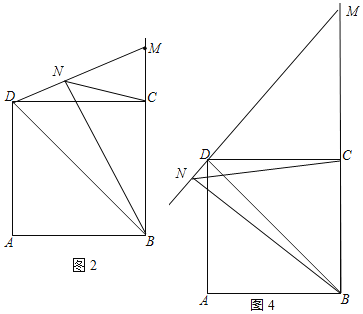
②线段NB,NC和ND之间的数量关系为:NB=ND+![]() NC,或
NC,或![]() NC=NB+ND.
NC=NB+ND.
理由如下:
当N在DM上时,在NB上截取BE=ND,

∵∠MCD=∠BNM=90°,
∴∠DMC+∠CDN=∠DMC+∠CBE=90°,
∴∠CDN=∠CBE,
在△CDN和△CBE中,
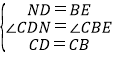 ,
,
∴△CDN≌△CBE(SAS),
∴NC=EC,∠DCN=∠BCE,
∴∠NCE=∠DCN+∠DCE=∠BCE+∠DCE=∠BCD=90°,
∴△NCE是等腰直角三角形,
∴NE=![]() NC,
NC,
∴NB=BE+NE=ND+![]() NC;
NC;
当N在MD延长线上时,延长NB至E,使BE=ND,

同理得:△CDN≌△CBE,
∴NC=EC,∠DCN=∠BCE,
∴∠NCE=∠DCN+∠DCE=∠BCE+∠DCE=∠BCD=90°,
∴△NCE是等腰直角三角形,
∴NE=![]() NC,
NC,
∵NE=NB+BE,
∴![]() NC=NB+ND.
NC=NB+ND.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】简答题:
(1)当![]() 为何值时,关于
为何值时,关于![]() 的方程
的方程![]() 是一元二次方程?
是一元二次方程?
(2)已知关于![]() 的一元二次方程
的一元二次方程![]() 有一个根是0,求
有一个根是0,求![]() 的值.
的值.
(3)在第(2)题中,如果要使已知方程有一个根是l,那么m应该等于什么数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】天空中有一个静止的广告气球C,从地面A点测得C点的仰角为45°,从地面B测得仰角为60°,已知AB=20米,点C和直线AB在同一铅垂平面上,求气球离地面的高度.(结果精确到0.1米)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿边
出发,沿边![]() 向点
向点![]() 以每秒2个单位长的速度运动,动点
以每秒2个单位长的速度运动,动点![]() 同时从点
同时从点![]() 出发,在边
出发,在边![]() 上以每秒1个单位长的速度向点
上以每秒1个单位长的速度向点![]() 运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为
运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为![]() (秒),
(秒),
(1)①设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 为何值时,
为何值时,![]() ?
?![]() 能不能等于
能不能等于![]() ?为什么?
?为什么?
(2)①当![]() 为何值时,
为何值时,![]() ?
?
②当![]() 为何值时,点
为何值时,点![]() 是在
是在![]() 的垂直平分线上?
的垂直平分线上?
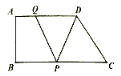
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,![]() 为正方形
为正方形![]() 的边
的边![]() 上一点,将正方形
上一点,将正方形![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,连接并延长
处,连接并延长![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(2)如图2,点![]() 分别在
分别在![]() 边上,且
边上,且![]() ,求证:
,求证:![]()
(3)如图3,点![]() 分别在
分别在![]() 边上,点
边上,点![]() 分别在
分别在![]() 边上,
边上,![]() 交
交![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店购进一批甲、乙两种款型衬衫,甲种款型共用了7800元,乙种款型共用了6400元,甲种款型的件数是乙种款型件数的1.5倍,甲种款型每件的进价比乙种款型每件的进价少30元.
(1)求甲、乙两种款型的衬衫各购进多少件?
(2)商店进价提高60%标价销售,销售一段时间后,甲款型全部售完,乙款型剩余一半,商店决定对乙款型剩余的按标价的五折降价销售,很快全部售完。求售完这批衬衫商店共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,运动到3秒钟时,两点相距15个单位长度.已知动点A、B的运动速度比之是3:2(速度单位:1个单位长度/秒).
(1)求两个动点运动的速度;
(2)A、B两点运动到3秒时停止运动,请在数轴上标出此时A、B两点的位置;
(3)若A、B两点分别从(2)中标出的位置再次同时开始在数轴上运动,运动的速度不变,运动的方向不限,问:经过几秒钟,A、B两点之间相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角三角形ABC中,∠ACB=90°,E为AB上一点,且CE=EB,ED⊥CB于D,则下列结论中不一定成立的是( )

A.AE=BEB.CE=![]() ABC.∠CEB=2∠AD.AC=
ABC.∠CEB=2∠AD.AC=![]() AB
AB
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com