
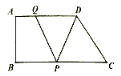
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发,沿边
出发,沿边![]() 向点
向点![]() 以每秒2个单位长的速度运动,动点
以每秒2个单位长的速度运动,动点![]() 同时从点
同时从点![]() 出发,在边
出发,在边![]() 上以每秒1个单位长的速度向点
上以每秒1个单位长的速度向点![]() 运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为
运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为![]() (秒),
(秒),
(1)①设![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
②当![]() 为何值时,
为何值时,![]() ?
?![]() 能不能等于
能不能等于![]() ?为什么?
?为什么?
(2)①当![]() 为何值时,
为何值时,![]() ?
?
②当![]() 为何值时,点
为何值时,点![]() 是在
是在![]() 的垂直平分线上?
的垂直平分线上?
【答案】(1)①S=﹣2t+12(0<t≤4.5);②S不能等于2;(2)①当t=3时,四边形PCDQ是平行四边形.②当t=![]() 时,点Q是在PD的垂直平分线上.
时,点Q是在PD的垂直平分线上.
【解析】
(1)①过点P作PE⊥AD于E,可得四边形ABPE是矩形,PE=AB=4,又因为DQ=6﹣t,可得![]() 与
与![]() 之间的函数关系式,根据
之间的函数关系式,根据![]() ,点
,点![]() 从点
从点![]() 出发,沿边
出发,沿边![]() 向点
向点![]() 以每秒2个单位长的速度运动,可得x取值范围;②设s=6,s=2即可解答;(2)①当PQ∥CD时,又因为 DQ∥CP,所以四边形PCDQ是平行四边形,可得PC=DQ,从而求解;②A因为E=BP=2t,PE=AB=4,QE=AE-AQ=BP-AQ=2t﹣t=t,所以当点Q是在PD的垂直平分线上时,DQ=PQ,DQ2=PQ2,根据勾股定理得t2+42=(6﹣t)2,从而求解.
以每秒2个单位长的速度运动,可得x取值范围;②设s=6,s=2即可解答;(2)①当PQ∥CD时,又因为 DQ∥CP,所以四边形PCDQ是平行四边形,可得PC=DQ,从而求解;②A因为E=BP=2t,PE=AB=4,QE=AE-AQ=BP-AQ=2t﹣t=t,所以当点Q是在PD的垂直平分线上时,DQ=PQ,DQ2=PQ2,根据勾股定理得t2+42=(6﹣t)2,从而求解.
(1)①直角梯形ABCD中,AD∥BC,∠A=90°,BC=9,AB=4,AD=6,
依题意AQ=t,BP=2t,则DQ=6﹣t,CP=9﹣2t,
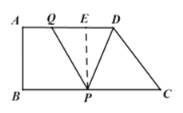
过点P作PE⊥AD于E,
则四边形ABPE是矩形,PE=AB=4,
∴S=![]() DQAB=
DQAB=![]() (6﹣t)×4=﹣2t+12(0<t≤4.5).
(6﹣t)×4=﹣2t+12(0<t≤4.5).
②当S=6时,﹣2t+12=6,
解得,t=3,
∴当t=3时,S=6,
当S=2时,﹣2t+12=2,
解得,t=5>4.5
∴S不能等于2;
(2)①当PQ∥CD时,∵DQ∥CP,
∴四边形PCDQ是平行四边形,∴PC=DQ,
∴9﹣2t=6﹣t解得:t=3,
∴当t=3时,四边形PCDQ是平行四边形.
②AE=BP=2t,PE=AB=4,
QE=AE-AQ=BP-AQ=2t﹣t=t,
当点Q是在PD的垂直平分线上时,DQ=PQ,DQ2=PQ2,
∴t2+42=(6﹣t)2,
解得:t=![]()
∴当t=![]() 时,点Q是在PD的垂直平分线上.
时,点Q是在PD的垂直平分线上.


 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
【题目】某一出租车一天下午以鼓楼为出发点在东西方向运营,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:![]() .
.
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知下列有理数:﹣(﹣3)、﹣4、0、+5、﹣![]()
(1)这些有理数中,整数有 个,非负数有 个.
(2)画数轴,并在数轴上表示这些有理数.
(3)把这些有理数用“<“号连接起来: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,与AC交于点D,点O是AB上一点,⊙O过B、D两点,且分别交AB、BC于点E、F.
(1)求证:AC是⊙O的切线;
(2)已知AB=10,BC=6,求⊙O的半径r.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 和
和![]() 有一条公共边
有一条公共边![]() ,且
,且![]() ,
,![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线.
的平分线.
(1)画出图形;
(2)若![]() ,
,![]() ,求
,求![]() 的大小;
的大小;
(3)通过对以上的解题回顾,你发现![]() 与
与![]() 、
、![]() 三个角之间有怎样的大小关系?请把你的发现结论直接写出来.
三个角之间有怎样的大小关系?请把你的发现结论直接写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,点M是直线BC上的一个动点(不与点B,C重合),作射线DM,过点B作BN⊥DM于点N,连接CN.
(1)如图1,当点M在BC上时,如果∠CDM=25°,那么∠MBN的度数是 .
(2)如图2,当点M在BC的延长线上时,
①依题意补全图2;
②用等式表示线段NB,NC和ND之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为16,则BE=( )
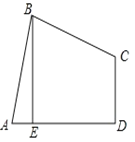
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(1)当![]() 为何值时,
为何值时,![]() ;
;
(2)当![]() 为何值时,
为何值时,![]() 的值比
的值比![]() 的值的
的值的![]() 大1;
大1;
(3)先填表,后回答:
|
|
|
| 0 | 1 | 2 | 3 | 4 |
| ||||||||
|
根据所填表格,回答问题:随着![]() 值的增大,
值的增大,![]() 的值逐渐 ;
的值逐渐 ;![]() 的值逐渐 .
的值逐渐 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com