
【题目】如图,在长方形ABCD中,DC=6cm,在DC上存在一点E,沿直线AE把三角形AE折叠,使点D恰好落在BC边上,设此点为F,若三角形ABF的面积为24,那么CE长度为__________cm2.

【答案】![]()
【解析】
由折叠可得∠D=∠AFE=90°,结合已知条件不难证明△ABF∽△FCE,由三角形相似的性质可以得出EC与CF的比值,根据比值分别设出EC、CF的长度,进而表示出EF、DE的长度,列方程解出x,进而求出CE的长度.
∵矩形ABCD,
∴AB=CD=6cm,∠B=∠C=∠D=90°,
∵S△ABF=![]() AB·BF=
AB·BF=![]() ×6BF=24,
×6BF=24,
∴BF=8,
由折叠可得∠AFE=∠D=90°,DE=EF,
∴∠AFB+∠EFC=90°,
∵∠AFB+∠BAF=90°,
∴∠EFC=∠BAF,
∵在△ABF与△FCE中,
![]() ,
,
∴△ABF∽△FCE,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
设CE=4xcm,CF=3xcm,则EF=ED=5xcm,
∴6=5x+4x,
∴x=![]() ,
,
∴CE=![]() cm.
cm.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】李明从市场上买回一块矩形铁皮,他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好能围成一个容积为15立方米的无盖长方体运输箱,且此长方体运输箱底面的长比宽多2米,现已知购买这种铁皮每平方米需20元,问购买这张矩形铁皮共花了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点 E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.
(1)求E点坐标;
(2)设抛物线的解析式为y=a(x﹣h)2+k,求a,h,k;
(3)点M为直线AB上一动点,点N为抛物线上一动点,是否存在点M,N,使得以点M,N,D,E为顶点的四边形是平行四边形?若存在,请直接写出满足条件的点M,N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AE⊥AB,且AE=AB,BC⊥CD且BC=CD,若点E、B、D到直线AC的距离分别为6,3,4,则图中实现所围成的图像面积是( )

A. 50 B. 44 C. 38 D. 32
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的两条角平分线BD、CE交于O,且∠A=60°,则下列结论中不正确的是( )
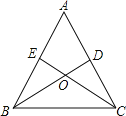
A.∠BOC=120° B.BC=BE+CD C.OD=OE D.OB=OC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y= ![]() x2(0≤x≤2)的图象记为曲线C1 , 将C1绕坐标原点O逆时针旋转90°,得曲线C2 .
x2(0≤x≤2)的图象记为曲线C1 , 将C1绕坐标原点O逆时针旋转90°,得曲线C2 . 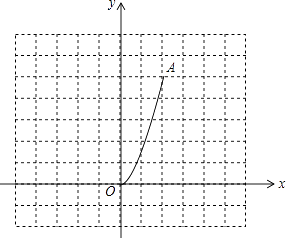
(1)请画出C2;
(2)写出旋转后A(2,5)的对应点A1的坐标;
(3)直接写出C1旋转至C2过程中扫过的面积 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“国美”、“苏宁”两家电器商场出售同样的空气净化器和过滤网,空气净化器和过滤网在两家商场的售价一样.已知买一个空气净化器和![]() 个过滤网要花费
个过滤网要花费![]() 元,买
元,买![]() 个空气净化器和
个空气净化器和![]() 个过滤网要花费
个过滤网要花费![]() 元.
元.
(![]() )请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
)请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
(![]() )为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买
)为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买![]() 个空气净化器和
个空气净化器和![]() 个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com