
【题目】如图,△ABC的两条角平分线BD、CE交于O,且∠A=60°,则下列结论中不正确的是( )
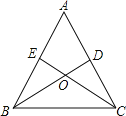
A.∠BOC=120° B.BC=BE+CD C.OD=OE D.OB=OC
【答案】D
【解析】
试题分析:根据三角形的内角和等于180°求出∠ABC+∠ACB=120°,再根据角平分线的性质求出∠OBC+∠OCB=60°,然后利用三角形的内角和等于180°列式计算即可求出∠BOC的度数;
连接OA,作OF⊥AB于点F,OG⊥AC于点G,OH⊥BC于点H,根据角平分线上的点到角的两边的距离相等可得OF=OG=OH,从而可得△BOF和△BOH全等,△COG和△COH全等,根据全等三角形对应边相等可得BH=BF,CH=CG,再根据四边形的内角和求出∠FOG=120°,根据对顶角相等求出∠EOD=120°,然后推出∠EOF=∠DOG,再利用“角边角”证明△EOF和△DOG全等,根据全等三角形对应边相等可得EF=DG,OD=OE,即可判定出B、C选项都正确,根据等角对等边的性质,只有∠ABC=∠ACB时才能得到OB=OC,所以D选项错误.
解:∵∠A=60°,
∴∠ABC+∠ACB=180°﹣∠A=180°﹣60°=120°,
∵△ABC的两条角平分线BD、CE交于O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣![]() (∠ABC+∠ACB)=120°,故A选项正确;
(∠ABC+∠ACB)=120°,故A选项正确;
如图,连接OA,作OF⊥AB于点F,OG⊥AC于点G,OH⊥BC于点H,
∵△ABC的两条角平分线BD、CE交于O,
∴OF=OG=OH,
利用“HL”可得△BOF≌△BOH,△COG≌△COH,
∴BH=BF,CH=CG,
在四边形AFOG中,∠FOG=360°﹣60°﹣90°×2=120°,
∴DOG=∠FOG﹣∠DOF=120°﹣∠DOF,
又∵∠EOD=∠BOC=120°,
∴∠EOF=∠EOD﹣∠DOF=120°﹣∠DOF,
∴∠EOF=∠DOG,
在△EOF和△DOG中,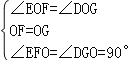 ,
,
∴△EOF≌△DOG(ASA),
∴EF=DG,OD=OE,故C选项正确;
∴BC=BH+CH=BF+CG=BE+EF+CD﹣DG=BE+CD,
即BC=BE+CD,故B选项正确;
只有当∠ABC=∠ACB时,∵△ABC的两条角平分线BD、CE交于O,
∴∠OBC=![]() ∠ABC,∠OCB=
∠ABC,∠OCB=![]() ∠ACB,
∠ACB,
∴∠OBC=∠OCB,
∴OB=OC,
而本题无法得到∠ABC=∠ACB,
所以,OB=OC不正确,故D选项错误.
故选D.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=1,则下列四个结论错误的是( ) 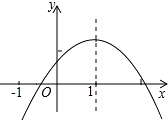
A.c>0
B.2a+b=0
C.b2﹣4ac>0
D.a﹣b+c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线L:y=ax2+bx+c与x轴交于A、B(3,0)两点(A在B的左侧),与y轴交于点C(0,3),已知对称轴x=1.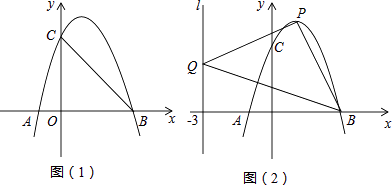
(1)求抛物线L的解析式;
(2)将抛物线L向下平移h个单位长度,使平移后所得抛物线的顶点落在△OBC内(包括△OBC的边界),求h的取值范围;
(3)设点P是抛物线L上任一点,点Q在直线l:x=﹣3上,△PBQ能否成为以点P为直角顶点的等腰直角三角形?若能,求出符合条件的点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)①在![]() 轴的正半轴上存在一点
轴的正半轴上存在一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
②在坐标轴上一共存在多少个点![]() ,使
,使![]() 成立?请直接写出符合条件的点
成立?请直接写出符合条件的点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,DC=6cm,在DC上存在一点E,沿直线AE把三角形AE折叠,使点D恰好落在BC边上,设此点为F,若三角形ABF的面积为24,那么CE长度为__________cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF,则旋转中心的坐标是( )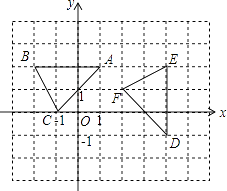
A.(0,0)
B.(1,0)
C.(1,﹣1)
D.(2.5,0.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两条平行直线上各有![]() 个点,用这
个点,用这![]() 个点按如下规则连接线段:
个点按如下规则连接线段:
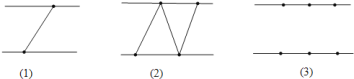
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出.
图![]() 展示了当
展示了当![]() 时的情况,此时图中三角形的个数为
时的情况,此时图中三角形的个数为![]() ;图
;图![]() 展示了当
展示了当![]() 时的一种情况,此时图中三角形的个数为
时的一种情况,此时图中三角形的个数为![]() .试回答下列问题:
.试回答下列问题:
![]() 当
当![]() 时,请在图
时,请在图![]() 中画出使三角形个数最少的图形,此时图中三角形的个数是________;
中画出使三角形个数最少的图形,此时图中三角形的个数是________;
![]() 试猜想当有
试猜想当有![]() 对点时,按上述规则画出的图形中,最少有________个三角形;
对点时,按上述规则画出的图形中,最少有________个三角形;
![]() 当
当![]() 时,按上述规则画出的图形中,最少有________个三角形.
时,按上述规则画出的图形中,最少有________个三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
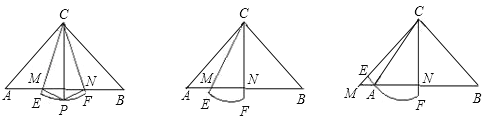
【题目】已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径长等于CA的扇形CEF绕点C旋转,直线CE、CF分别与直线AB交于点M、N.
(1)如图①,当AM=BN时,将△ACM沿CM折叠,点A落在弧EF的中点P处,再将△BCN沿CN折叠,点B也恰好落在点P处,此时,PM=AM,PN=BN,△PMN的形状是 .线段AM、BN、MN之间的数量关系是 ;
(2)如图②,当扇形CEF绕点C在∠ACB内部旋转时,线段MN、AM、BN之间的数量关系是 .试证明你的猜想;
(3)当扇形CEF绕点C旋转至图③的位置时,线段MN、AM、BN之间的数量关系是 .(不要求证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com