
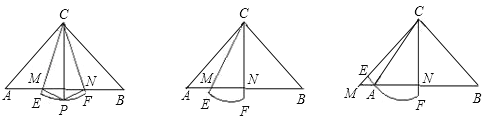
【题目】已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径长等于CA的扇形CEF绕点C旋转,直线CE、CF分别与直线AB交于点M、N.
(1)如图①,当AM=BN时,将△ACM沿CM折叠,点A落在弧EF的中点P处,再将△BCN沿CN折叠,点B也恰好落在点P处,此时,PM=AM,PN=BN,△PMN的形状是 .线段AM、BN、MN之间的数量关系是 ;
(2)如图②,当扇形CEF绕点C在∠ACB内部旋转时,线段MN、AM、BN之间的数量关系是 .试证明你的猜想;
(3)当扇形CEF绕点C旋转至图③的位置时,线段MN、AM、BN之间的数量关系是 .(不要求证明)
科目:初中数学 来源: 题型:
【题目】如图,△ABC的两条角平分线BD、CE交于O,且∠A=60°,则下列结论中不正确的是( )
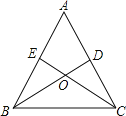
A.∠BOC=120° B.BC=BE+CD C.OD=OE D.OB=OC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用直尺和圆规作一个角等于已知角的作法如下:
①以点O为圆心,以任意长为半径画弧,分别交OA、OB于点D、C;
②作射线O′B′,以点O′为圆心,以 长为半径画弧,交O′B′于点C′;
③以点C′为圆心,以 长为半径画弧,两弧交于点D′;
④过点D′作射线O′A′,∴∠A′O′B′为所求.
(1)请将上面的作法补充完整;
(2)△OCD≌△O′C′D′的依据是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=3x﹣3分别交x轴,y轴于A,B两点,抛物线y=x2+bx+c经过A,B两点,点C是抛物线与x轴的另一个交点(与点A不重合),点D是抛物线的顶点,请解答下列问题. 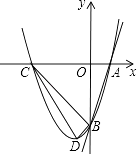
(1)求抛物线的解析式;
(2)判断△BCD的形状,并说明理由;
(3)求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“国美”、“苏宁”两家电器商场出售同样的空气净化器和过滤网,空气净化器和过滤网在两家商场的售价一样.已知买一个空气净化器和![]() 个过滤网要花费
个过滤网要花费![]() 元,买
元,买![]() 个空气净化器和
个空气净化器和![]() 个过滤网要花费
个过滤网要花费![]() 元.
元.
(![]() )请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
)请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
(![]() )为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买
)为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买![]() 个空气净化器和
个空气净化器和![]() 个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
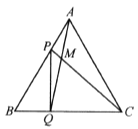
【题目】如图,点P,Q分别是边长为4 cm的等边三角形ABC边AB,BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1 cm/s,连接AQ,CP,相交于点M.下面四个结论正确的有________(填序号).①BP=CM; ②△ABQ ≌△CAP ;③∠CMQ的度数不变,始终等于60;④当第![]() s或
s或![]() s时,△PBQ为直角三角形.
s时,△PBQ为直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1和图2中的正方形ABCD和四边形AEFG都是正方形. 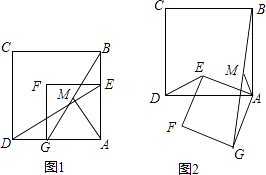
(1)如图1,连接DE,BG,M为线段BG的中点,连接AM,探究AM与DE的数量关系和位置关系,并证明你的结论;
(2)在图1的基础上,将正方形AEFG绕点A逆时针方向旋转到图2的位置,连结DE、BG,M为线段BG的中点,连结AM,探究AM与DE的数量关系和位置关系,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com