
【题目】如图,已知直线y=3x﹣3分别交x轴,y轴于A,B两点,抛物线y=x2+bx+c经过A,B两点,点C是抛物线与x轴的另一个交点(与点A不重合),点D是抛物线的顶点,请解答下列问题. 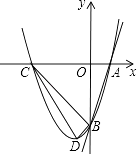
(1)求抛物线的解析式;
(2)判断△BCD的形状,并说明理由;
(3)求△BCD的面积.
【答案】
(1)解:∵直线y=3x﹣3分别交x轴,y轴于A,B两点,
当y=0时,x=1,当x=0时,y=﹣3,
∴点A(1,0),点B(0,﹣3),
∵抛物线y=x2+bx+c经过A,B两点,
∴ ![]() ,
,
解得, ![]() ,
,
∴抛物线的解析式为:y=x2+2x﹣3
(2)解:△BCD是直角三角形,
理由:∵y=x2+2x﹣3=(x+1)2﹣4=(x+3)(x﹣1),
∴当y=0时,x=﹣3或x=1,此抛物线的顶点坐标是(﹣1,﹣4),
∵抛物线y=x2+bx+c经过A,B两点,点C是抛物线与x轴的另一个交点(与点A不重合),点D是抛物线的顶点,
∴点C(﹣3,0),点D(﹣1,﹣4),
∵点B(0,﹣3),
∴BC= ![]() =3
=3 ![]() ,
,
CD= ![]() =2
=2 ![]() ,
,
BD= ![]() =
= ![]() ,
,
∵ ![]() ,
,
∴BC2+BD2=CD2,
∴△BCD是直角三角形
(3)解:由(2)知△BCD是直角三角形,∠CBD=90°, ![]() ,CD=2
,CD=2 ![]() ,BD=
,BD= ![]() ,
,
∴△BCD的面积是: ![]() ,
,
即△BCD的面积是3
【解析】(1)根据直线y=3x﹣3分别交x轴,y轴于A,B两点,可以求得点A和点B的坐标,由抛物线y=x2+bx+c经过A,B两点,从而可以得到抛物线的解析式;(2)根据(1)中的函数解析式可以分别求得点C和点D的坐标,从而可以求得BC、BD、CD的长,然后根据勾股定理的逆定理即可解答本题;(3)根据(2)中的判断,然后根据三角形的面积公式即可解答本题.
【考点精析】本题主要考查了抛物线与坐标轴的交点的相关知识点,需要掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)①在![]() 轴的正半轴上存在一点
轴的正半轴上存在一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
②在坐标轴上一共存在多少个点![]() ,使
,使![]() 成立?请直接写出符合条件的点
成立?请直接写出符合条件的点![]() 的坐标.
的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两条平行直线上各有![]() 个点,用这
个点,用这![]() 个点按如下规则连接线段:
个点按如下规则连接线段:
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①要求的线段必须全部画出.
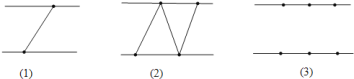
图![]() 展示了当
展示了当![]() 时的情况,此时图中三角形的个数为
时的情况,此时图中三角形的个数为![]() ;图
;图![]() 展示了当
展示了当![]() 时的一种情况,此时图中三角形的个数为
时的一种情况,此时图中三角形的个数为![]() .试回答下列问题:
.试回答下列问题:
![]() 当
当![]() 时,请在图
时,请在图![]() 中画出使三角形个数最少的图形,此时图中三角形的个数是________;
中画出使三角形个数最少的图形,此时图中三角形的个数是________;
![]() 试猜想当有
试猜想当有![]() 对点时,按上述规则画出的图形中,最少有________个三角形;
对点时,按上述规则画出的图形中,最少有________个三角形;
![]() 当
当![]() 时,按上述规则画出的图形中,最少有________个三角形.
时,按上述规则画出的图形中,最少有________个三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).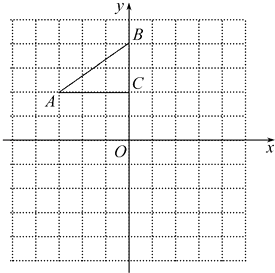
(1)将△ABC以点O为旋转中心旋转90°,请画出旋转后的△A′B′C′;
(2)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平面直角坐标系中,△ABC的边AB在x轴上,∠C=60°,AC交y轴于点E,AC,BC的长是方程x2﹣16x+64=0的两个根且OA:OB=1:3,请解答下列问题: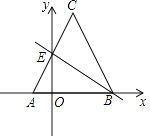
(1)求点C的坐标;
(2)求直线EB的解析式;
(3)在x轴上是否存在点P,使△BEP为等腰三角形?若存在,请直接写出点P的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
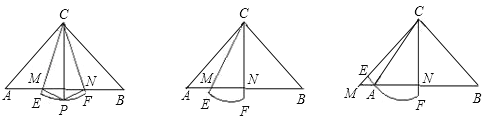
【题目】已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径长等于CA的扇形CEF绕点C旋转,直线CE、CF分别与直线AB交于点M、N.
(1)如图①,当AM=BN时,将△ACM沿CM折叠,点A落在弧EF的中点P处,再将△BCN沿CN折叠,点B也恰好落在点P处,此时,PM=AM,PN=BN,△PMN的形状是 .线段AM、BN、MN之间的数量关系是 ;
(2)如图②,当扇形CEF绕点C在∠ACB内部旋转时,线段MN、AM、BN之间的数量关系是 .试证明你的猜想;
(3)当扇形CEF绕点C旋转至图③的位置时,线段MN、AM、BN之间的数量关系是 .(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
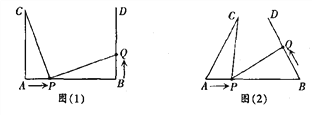
【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D. 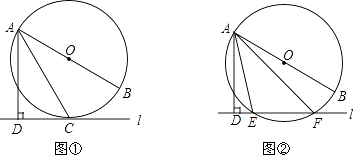
(1)如图①,当直线l与⊙O相切于点C时,求证:AC平分∠DAB;
(2)如图②,当直线l与⊙O相交于点E,F时,求证:∠DAE=∠BAF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com