
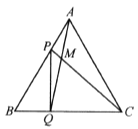
【题目】如图,点P,Q分别是边长为4 cm的等边三角形ABC边AB,BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1 cm/s,连接AQ,CP,相交于点M.下面四个结论正确的有________(填序号).①BP=CM; ②△ABQ ≌△CAP ;③∠CMQ的度数不变,始终等于60;④当第![]() s或
s或![]() s时,△PBQ为直角三角形.
s时,△PBQ为直角三角形.
【答案】②③④
【解析】
由三角形ABC为等边三角形,得到三边相等,且内角为60°,根据题意得到AP=BQ,利用SAS得到三角形ABQ与三角形CAP全等;由全等三角形对应角相等得到∠AQB=∠CPA,利用三角形内角和定理即可确定出∠CMQ的度数不变,始终等于60°;分∠QPB与∠PQB为直角两种情况求出t的值,即可作出判断.
BP不一定等于CM,选项①错误;
根据题意得:AP=BQ=t,
∵△ABC为等边三角形,
∴![]()
在△ABQ和△CAP中,
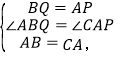
∴△ABQ≌△CAP(SAS),选项②正确;
∴∠AQB=∠CPA,
在△APM中,![]()
∵![]()
在△ABQ中,![]()
∴![]()
∴![]()
∴![]() ,选项③正确;
,选项③正确;
若![]() ,由
,由![]() ,得到PB=2BQ,即4t=2t,
,得到PB=2BQ,即4t=2t,
解得:t=![]() ;
;
若![]() ,由
,由![]() ,得到BQ=2PB,即t=2(4t),
,得到BQ=2PB,即t=2(4t),
解得:t=![]() ,
,
综上,当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形,选项④正确,
秒时,△PBQ为直角三角形,选项④正确,
故答案为:②③④


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC顶点的横、纵坐标都是整数.若将△ABC以某点为旋转中心,顺时针旋转90°得到△DEF,则旋转中心的坐标是( )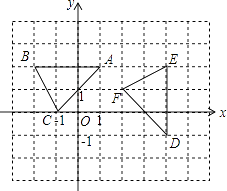
A.(0,0)
B.(1,0)
C.(1,﹣1)
D.(2.5,0.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).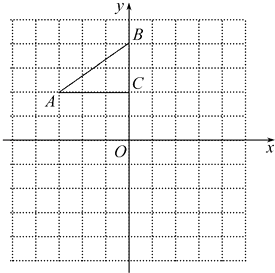
(1)将△ABC以点O为旋转中心旋转90°,请画出旋转后的△A′B′C′;
(2)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
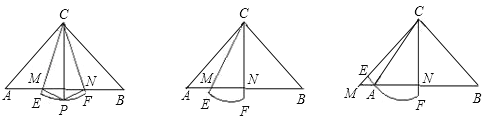
【题目】已知Rt△ABC中,∠ACB=90°,CA=CB,有一个圆心角为45°,半径长等于CA的扇形CEF绕点C旋转,直线CE、CF分别与直线AB交于点M、N.
(1)如图①,当AM=BN时,将△ACM沿CM折叠,点A落在弧EF的中点P处,再将△BCN沿CN折叠,点B也恰好落在点P处,此时,PM=AM,PN=BN,△PMN的形状是 .线段AM、BN、MN之间的数量关系是 ;
(2)如图②,当扇形CEF绕点C在∠ACB内部旋转时,线段MN、AM、BN之间的数量关系是 .试证明你的猜想;
(3)当扇形CEF绕点C旋转至图③的位置时,线段MN、AM、BN之间的数量关系是 .(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
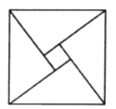
【题目】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图).如果大正方形的面积是100,小正方形的面积是4,直角三角形较短的直角边长为![]() ,较长的直角边长为
,较长的直角边长为![]() ,那么
,那么![]() 的值是_________.
的值是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
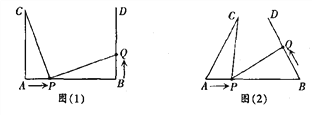
【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).
(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由,并判断此时线段PC和线段PQ的位置关系;
(2)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”为改“∠CAB=∠DBA=60°”,其他条件不变.设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
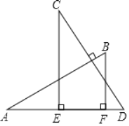
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的边AB在x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物线y=x2+bx+c经过A、C两点.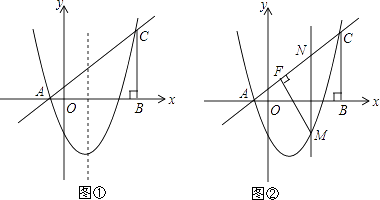
(1)求抛物线的解析式及其顶点坐标;
(2)如图①,点P是抛物线上位于x轴下方的一点,点Q与点P关于抛物线的对称轴对称,过点P,Q分别向x轴作垂线,垂足为点D,E,记矩形DPQE的周长为d,求d的最大值,并求出使d最大值时点P的坐标;
(3)如图②,点M是抛物线上位于直线AC下方的一点,过点M作MF⊥AC于点F,连接MC,作MN∥BC交直线AC于点N,若MN将△MFC的面积分成2:3两部分,请确定M点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某学习小组在探究三角形全等时,发现了下面这种典型的基本图形.如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线L经过点A,BD⊥直线L,CE⊥直线L,垂足分别为点D、E.证明:DE=BD+CE.
(2)组员小刘想,如果三个角不是直角,那结论是否会成立呢?如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线L上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图③,过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,AH是BC边上的高,延长HA交EG于点I,求证:I是EG的中点.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com