
【题目】现在的青少年由于沉迷电视、手机、网络游戏等,视力日渐减退,某市为了解学生的视力变化情况,从全市九年级随机抽取了1500名学生,统计了每个人连续三年视力检查的结果,根据视力在4.9以下的人数变化制成折线统计图,并对视力下降的主要因素进行调查,制成扇形统计图.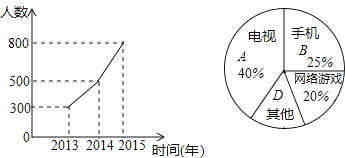
解答下列问题:
(1)图中D所在扇形的圆心角度数为 ;
(2)若2015年全市共有30000名九年级学生,请你估计视力在4.9以下的学生约有多少名?
(3)根据扇形统计图信息,你觉得中学生应该如何保护视力?
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】自从2012年12月4日中央公布“八项规定”以来,我市某中学积极开展“厉行勤俭节约,反对铺张浪费”的活动.为此,校学生会在全校范围内随机抽取了若干名学生就某日晚饭浪费饭菜情况进行调查,调查内容分为四种:A.饭和菜全部吃完;B.有剩饭但菜吃完;C.饭吃完但菜有剩;D.饭和菜都有剩.学生会根据统计结果绘制了如下统计表和统计图,根据所提供的信息回答下列问题:
选项 | 频数 | 频率 |
A | 30 | M |
B | n | 0.2 |
C | 5 | 0.1 |
D | 5 | 0.1 |

(1)这次被抽查的学生有多少人?
(2)求表中m,n的值,并补全条形统计图;
(3)该中学有学生2200名,请估计这餐晚饭有剩饭的学生人数,按平均每人剩10克米饭计算,这餐晚饭将浪费多少千克米饭?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,点E、F是AD上的点,且AE=EF=FD.连接BE、BF,使它们分别与AO相交于点G、H.
(1)(1)求EG:BG的值;
(2)(2)求证:AG=OG;
(3)(3)设AG=a,GH=b,HO=c,求a:b:c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC切⊙O于点B,OC平行于弦AD,过点D作DE⊥AB于点E,连结AC,与DE交于点P.求证: 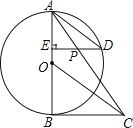
(1)PE=PD
(2)ACPD=APBC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中.顶点为(﹣4,﹣1)的抛物线交y轴于点A(0,3),交x轴于B,C两点.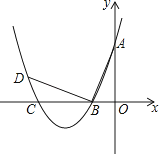
(1)求此抛物线的解析式;
(2)已知点P是抛物线上位于B,C两点之间的一个动点,问:当点P运动到什么位置时,四边形ABPC的面积最大?并求出此时四边形ABPC的面积.
(3)过点B作AB的垂线交抛物线于点D,是否存在以点C为圆心且与线段BD和抛物线的对称轴l同时相切的圆?若存在,求出圆的半径;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD,它们都与地面垂直,为了测得电线杆的高度,一个小组的同学进行了如下测量:某一时刻,在太阳光照射下,旗杆落在围墙上的影子EF的长度为2米,落在地面上的影子BF的长为10米,而电线杆落在围墙上的影子GH的长度为3米,落在地面上的影子DH的长为5米,依据这些数据,该小组的同学计算出了电线杆的高度.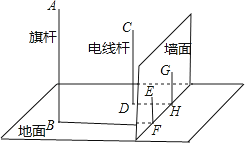
(1)该小组的同学在这里利用的是 投影的有关知识进行计算的;
(2)试计算出电线杆的高度,并写出计算的过程。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在第一象限内,点P(2,3),M(a,2)是双曲线y=![]() (k≠0)上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为
(k≠0)上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,“在初中数学教学中使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了若干名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果绘制成如下不完整的统计表和统计图:
学生对使用计算器影响计算能力发展的看法统计表
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数 | 100 | 60 | m |
根据以上图表信息,解答下列问题: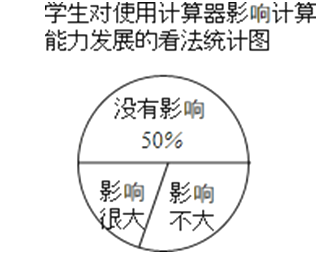
(1)统计表中的m= ;
(2)统计图中表示“影响不大”的扇形的圆心角度数为 度;
(3)从这次接受调查的学生中随机调查一人,恰好是持“影响很大”看法的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com