
ЁОЬтФПЁПШчЭМ1ЃЌдкЬнаЮABCDжаЃЌADЁЮBCЃЌЁЯABCЃН90ЁуЃЌcosCЃН![]() ЃЌDCЃН5ЃЌBCЃН6ЃЌвдЕуBЮЊдВаФЃЌBDЮЊАыОЖзїдВЛЁЃЌЗжБ№НЛБпCDЁЂBCгкЕуEЁЂFЃЎ
ЃЌDCЃН5ЃЌBCЃН6ЃЌвдЕуBЮЊдВаФЃЌBDЮЊАыОЖзїдВЛЁЃЌЗжБ№НЛБпCDЁЂBCгкЕуEЁЂFЃЎ
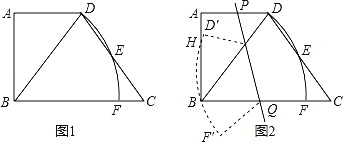
ЃЈ1ЃЉЧѓsinЁЯBDCЕФжЕЃЛ
ЃЈ2ЃЉСЊНсBEЃЌЩшЕуGЮЊЩфЯпDBЩЯвЛЖЏЕуЃЌШчЙћЁїADGЯрЫЦгкЁїBECЃЌЧѓDGЕФГЄЃЛ
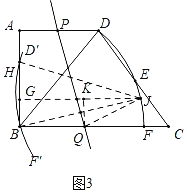
ЃЈ3ЃЉШчЭМ2ЃЌЕуPЁЂQЗжБ№ЮЊБпADЁЂBCЩЯЖЏЕуЃЌНЋЩШаЮDBFбизХжБЯпPQелЕўЃЌелЕўКѓЕФЛЁD'F'ОЙ§ЕуBгыABЩЯЕФвЛЕуHЃЈЕуDЁЂFЗжБ№ЖдгІЕуD'ЃЌF'ЃЉЃЌЩшBHЃНxЃЌBQЃНyЃЌЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЈВЛашвЊаДЖЈвхгђЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉyЃН
ЃЛЃЈ3ЃЉyЃН![]()
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1жаЃЌСЌНгBEЃЌЙ§ЕуDзїDKЁЭBCгкKЃЌЙ§ЕуBзїBJЁЭCDгкJЃЎЯыАьЗЈЧѓГіBJЃЌBDМДПЩНтОіЮЪЬтЃЎ
ЃЈ2ЃЉЗжСНжжЧщаЮЗжБ№ЧѓНтЃКЂйЕБЁїADGЁзЁїBCEЪБЃЎЂкЕБЁїADGЁзЁїECBЪБЃЌЗжБ№РћгУЯрЫЦШ§НЧаЮЕФаджЪЧѓНтМДПЩЃЎ
ЃЈ3ЃЉШчЭМ3жаЃЌЙ§ЕуBзїBJЁЭPQНЛ![]() гкJЃЌСЌНгBJЃЌJHЃЌJQЃЌЙ§ЕуJзїJGЁЭBHгкGЃЌЙ§ЕуQзїQKЁЭJHгкKЃЎгЩЬтвтBQЃНQJЃНyЃЌЧѓГіQKЃЌKJЃЌдкRtЁїQKJжаЃЌРћгУЙДЙЩЖЈРэМДПЩНтОіЮЪЬтЃЎ
гкJЃЌСЌНгBJЃЌJHЃЌJQЃЌЙ§ЕуJзїJGЁЭBHгкGЃЌЙ§ЕуQзїQKЁЭJHгкKЃЎгЩЬтвтBQЃНQJЃНyЃЌЧѓГіQKЃЌKJЃЌдкRtЁїQKJжаЃЌРћгУЙДЙЩЖЈРэМДПЩНтОіЮЪЬтЃЎ
ЃЈ1ЃЉШчЭМ1жаЃЌСЌНгBEЃЌЙ§ЕуDзїDKЁЭBCгкKЃЌЙ§ЕуBзїBJЁЭCDгкJЃЎ
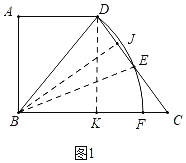
дкRtЁїCDKжаЃЌЁпЁЯDKCЃН90ЁуЃЌCDЃН5ЃЌcosЁЯCЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрCKЃН3ЃЌ
ЁпBCЃН6ЃЌ
ЁрBKЃНCKЃН3ЃЌ
ЁпADЁЮBCЃЌЁЯABCЃН90ЁуЃЌ
ЁрЁЯAЃН90Ёу
ЁпDKЁЭBCЃЌ
ЁрЁЯAЃНЁЯABCЃНЁЯDKBЃН90ЁуЃЌ
ЁрЫФБпаЮABKDЪЧОиаЮЃЌ
ЁрADЃНBKЃН3ЃЌ
ЁрDBЃНDCЃН5ЃЌDKЃН![]() ЃН
ЃН![]() ЃН4ЃЌ
ЃН4ЃЌ
ЁпSЁїDCBЃН![]() BCDKЃН
BCDKЃН![]() CDBJЃЌ
CDBJЃЌ
ЁрBJЃН![]() ЃЌ
ЃЌ
ЁрDJЃН![]() ЃН
ЃН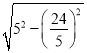 ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпBDЃНBEЃЌBJЁЭDEЃЌ
ЁрDJЃНJEЃН![]() ЃЌ
ЃЌ
ЁрECЃНCDЉDJЃНJEЃН5Љ![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрsinЁЯBDCЃН![]() ЃН
ЃН![]() ЃН
ЃН![]() ЃЎ
ЃЎ
ЃЈ2ЃЉШчЭМ2жаЃЌ
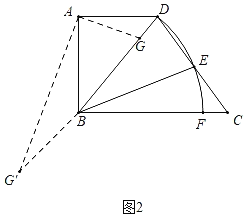
ЁпADЁЮBCЃЌ
ЁрЁЯADGЃНЁЯDBCЃЌ
ЁпDBЃНDCЃЌ
ЁрЁЯDBCЃНЁЯCЃЌ
ЁрЁЯADGЃНЁЯCЃЌ
ЁпЁїADGЯрЫЦЁїBECЃЌ
ЁргаСНжжЧщаЮЃКЕБЁїADGЁзЁїBCEЪБЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрDGЃН![]() ЃЌ
ЃЌ
ЕБЁїADGЁзЁїECBЪБЃЌ
![]() ЃН
ЃН![]() ЃЌ
ЃЌ
![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁрDGЃН![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШчЭМ3жаЃЌЙ§ЕуBзїBJЁЭPQНЛ![]() гкJЃЌСЌНгBJЃЌJHЃЌJQЃЌЙ§ЕуJзїJGЁЭBHгкGЃЌЙ§ЕуQзїQKЁЭJHгкKЃЎ
гкJЃЌСЌНгBJЃЌJHЃЌJQЃЌЙ§ЕуJзїJGЁЭBHгкGЃЌЙ§ЕуQзїQKЁЭJHгкKЃЎ
гЩЬтвтЃКQBЃНQJЃНyЃЌBJЃНBDЃН5ЃЌ
ЁпJBЃНJHЃЌJGЁЭBHЃЌ
ЁрBGЃНGHЃН![]() xЃЌ
xЃЌ
ЁрJGЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпЁЯGBQЃНЁЯBGKЃНЁЯQKGЃН90ЁуЃЌ
ЁрЫФБпаЮBGKQЪЧОиаЮЃЌ
ЁрBQЃНGKЃНyЃЌQKЃНGBЃН![]() xЃЌ
xЃЌ
дкRtЁїQKJжаЃЌ
ЁпJQ2ЃНQK2+KJ2ЃЌ
Ёрy2ЃН![]() x2+ЃЈ
x2+ЃЈ![]() ЉyЃЉ2ЃЌ
ЉyЃЉ2ЃЌ
ЁрyЃН![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌСљБпаЮ![]() ЪЧе§СљБпаЮЃЌЕу
ЪЧе§СљБпаЮЃЌЕу![]() ЪЧБп
ЪЧБп![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЗжБ№гы
ЗжБ№гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌдђ
ЃЌдђ![]() ЫФБпаЮMCDNЕФжЕЮЊЃЈ ЃЉ
ЫФБпаЮMCDNЕФжЕЮЊЃЈ ЃЉ

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
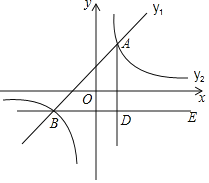
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЗДБШР§КЏЪ§
ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкЕу
ЕФЭМЯѓНЛгкЕу![]() КЭ
КЭ![]() ЃЎ
ЃЎ
![]() ЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
![]() ЧыжБНгаДГі
ЧыжБНгаДГі![]() ЪБЃЌxЕФШЁжЕЗЖЮЇЃЛ
ЪБЃЌxЕФШЁжЕЗЖЮЇЃЛ
![]() Й§ЕуBзї
Й§ЕуBзї![]() жсЃЌ
жсЃЌ![]() гкЕуDЃЌЕуCЪЧжБЯпBEЩЯвЛЕуЃЌШє
гкЕуDЃЌЕуCЪЧжБЯпBEЩЯвЛЕуЃЌШє![]() ЃЌЧѓЕуCЕФзјБъЃЎ
ЃЌЧѓЕуCЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓНЛ
ЕФЭМЯѓНЛ![]() жсгк
жсгк![]() СНЕуЃЌНЛ
СНЕуЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЖЅЕу
ЃЌЖЅЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНКЭжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕу![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯЕФвЛИіЖЏЕуЃЌЙ§Еу
ЩЯЕФвЛИіЖЏЕуЃЌЙ§Еу![]() зї
зї![]() жсЕФДЙЯпЃЌНЛХзЮяЯпгкЕу
жсЕФДЙЯпЃЌНЛХзЮяЯпгкЕу![]() ЃЌЕБЕу
ЃЌЕБЕу![]() дкЕквЛЯѓЯоЪБЃЌЧѓЯпЖЮ
дкЕквЛЯѓЯоЪБЃЌЧѓЯпЖЮ![]() ГЄЖШЕФзюДѓжЕЃЛ
ГЄЖШЕФзюДѓжЕЃЛ
ЃЈ3ЃЉдкХзЮяЯпЩЯЪЧЗёДцдквьгк![]() ЕФЕу
ЕФЕу![]() ЃЌЪЙ
ЃЌЪЙ![]() жа
жа![]() БпЩЯЕФИпЮЊ
БпЩЯЕФИпЮЊ![]() ЃЌШєДцдкЧѓГіЕу
ЃЌШєДцдкЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌACЃН6ЃЌBCЃН8ЃЌЕуDЁЂEЗжБ№ЪЧБпBCЁЂABЩЯвЛЕуЃЌDEЁЮACЃЌBDЃН5![]() ЃЌАбЁїBDEШЦзХЕуBа§зЊЕУЕНЁїBD'E'ЃЈЕуDЁЂEЗжБ№гыЕуD'ЃЌE'ЖдгІЃЉЃЌШчЙћЕуAЃЌD'ЁЂE'дкЭЌвЛжБЯпЩЯЃЌФЧУДAE'ЕФГЄЮЊ_____ЃЎ
ЃЌАбЁїBDEШЦзХЕуBа§зЊЕУЕНЁїBD'E'ЃЈЕуDЁЂEЗжБ№гыЕуD'ЃЌE'ЖдгІЃЉЃЌШчЙћЕуAЃЌD'ЁЂE'дкЭЌвЛжБЯпЩЯЃЌФЧУДAE'ЕФГЄЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=CBЃЌЁЯABC=90ЁуЃЌDЮЊABбгГЄЯпЩЯвЛЕуЃЌЕуEдкBCБпЩЯЃЌЧвBE=BDЃЌСЌНсAEЁЂDEЁЂDC

ЂйЧѓжЄЃКЁїABEЁеЁїCBDЃЛ
ЂкШєЁЯCAE=30ЁуЃЌЧѓЁЯBDCЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
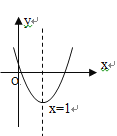
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯёШчЭМЫљЪОЃЌЖдГЦжсЪЧжБЯпx=1ЃЌЯТСаНсТлжаЃКЂйabc>0ЃЌЂк2a+b=0ЃЌЂл
ЕФЭМЯёШчЭМЫљЪОЃЌЖдГЦжсЪЧжБЯпx=1ЃЌЯТСаНсТлжаЃКЂйabc>0ЃЌЂк2a+b=0ЃЌЂл![]() <0ЃЌЂм4a+2b+c>0,Цфжае§ШЗЕФЪЧЃЈ ЃЉ
<0ЃЌЂм4a+2b+c>0,Цфжае§ШЗЕФЪЧЃЈ ЃЉ
A. ЂйЂкB. ЂйЂлC. ЂкЂлD. ЂкЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫСЫНтИпгЪЪаЁАаТЙкЗЮбзЁБвпЧщЗРПиЦкМфОХФъМЖбЇЩњЯпЩЯбЇЯАЧщПіЃЌЭЈЙ§ЮЪОэЭјОЭЁАФуЖдздМКЯпЩЯбЇЯАЕФаЇЙћЦРМлЁБНјааСЫЮЪОэЕїВщЃЌДгжаЫцЛњГщШЁСЫВПЗжбљОэНјааЭГМЦЃЌЛцжЦСЫШчЯТЕФЭГМЦЭМ
ИљОнЭГМЦЭМаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
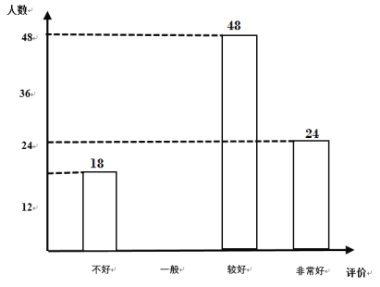
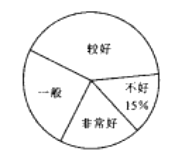
ЃЈ1ЃЉБОДЮЕїВщЕФбљБОШнСПЮЊЁЁЁЁЁЁЁЁЃЛ
ЃЈ2ЃЉЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉЩШаЮЭГМЦЭМжаЁАНЯКУЁБЖдгІЕФЩШаЮдВаФНЧЕФЖШЪ§ЮЊЁЁЁЁЁЁЁЁ![]() ЃЛ
ЃЛ
ЃЈ4ЃЉШєШЋЪаОХФъМЖЯпЩЯбЇЯАШЫЪ§га![]() ШЫЃЌЧыЙРМЦЖдЯпЩЯбЇЯАЦРМлЁАЗЧГЃКУЁБЕФШЫЪ§ЃЎ
ШЫЃЌЧыЙРМЦЖдЯпЩЯбЇЯАЦРМлЁАЗЧГЃКУЁБЕФШЫЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧЖўДЮКЏЪ§y=ax2+bx+cЃЈaЃЌbЃЌcЪЧГЃЪ§ЃЌaЁй0ЃЉЭМЯѓЕФвЛВПЗжЃЌгыxжсЕФНЛЕуAдкЕуЃЈ2ЃЌ0ЃЉКЭЃЈ3ЃЌ0ЃЉжЎМфЃЌЖдГЦжсЪЧx=1ЃЎЖдгкЯТСаЫЕЗЈЃКЂйabЃМ0ЃЛЂк2a+b=0ЃЛЂл3a+cЃО0ЃЛЂмa+bЁнmЃЈam+bЃЉЃЈmЮЊЪЕЪ§ЃЉЃЛЂнЕБЉ1ЃМxЃМ3ЪБЃЌyЃО0ЃЌЦфжае§ШЗЕФЪЧЃЈЁЁЁЁЃЉ

A. ЂйЂкЂм B. ЂйЂкЂн C. ЂкЂлЂм D. ЂлЂмЂн
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com